What Is -3x+1 Subtracted From 3x-1
News Co
Apr 20, 2025 · 4 min read
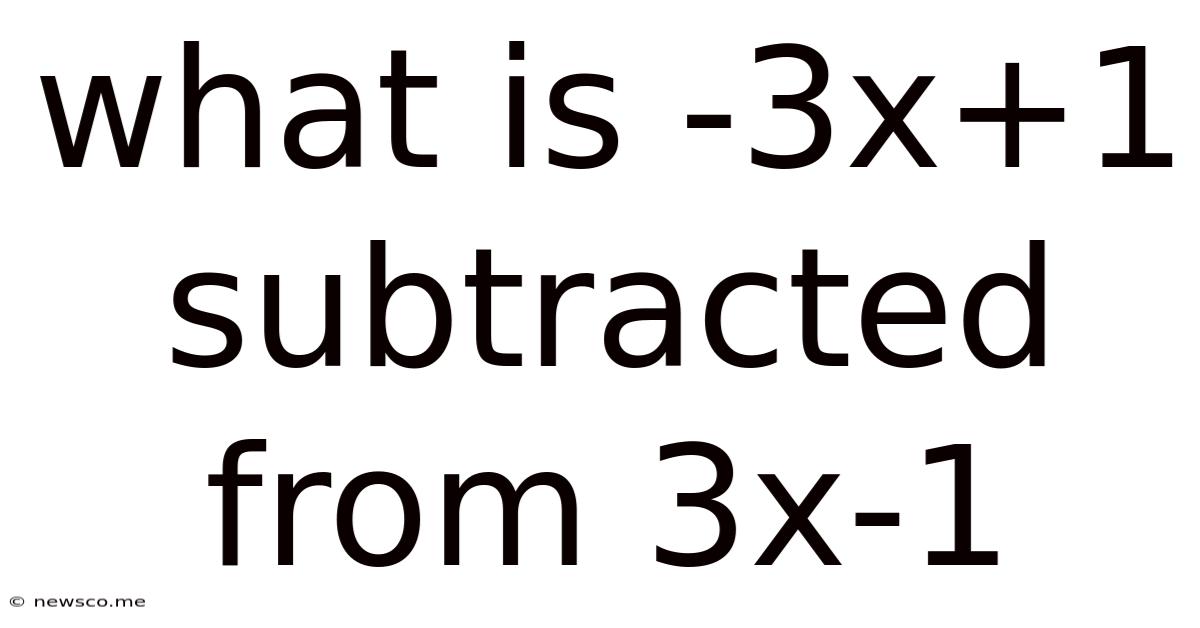
Table of Contents
What is 3x - 1 Subtracted from 3x - 1? Unraveling the Mystery of Subtraction in Algebra
This seemingly simple question, "What is 3x - 1 subtracted from 3x - 1?", opens the door to a deeper understanding of algebraic subtraction and the nuances of working with variables and constants. While the immediate answer might seem obvious, a thorough exploration reveals crucial concepts for anyone navigating the world of algebra. Let's delve into the intricacies of this problem and unlock its underlying principles.
Understanding Subtraction in Algebra
Before tackling the specific problem, let's solidify our understanding of subtraction in the context of algebra. Subtraction, fundamentally, is the inverse operation of addition. When we subtract a quantity from another, we're essentially adding the opposite of that quantity. This is a critical concept that simplifies many algebraic manipulations.
For example, subtracting 5 from 10 can be represented as 10 - 5 = 5. Alternatively, we can think of it as adding the opposite of 5, which is -5: 10 + (-5) = 5. This seemingly minor distinction becomes immensely powerful when dealing with variables and expressions.
Deconstructing the Problem: 3x - 1 Subtracted from 3x - 1
The core question is: (3x - 1) - (3x - 1) = ?
This problem presents a subtraction of algebraic expressions. To solve this, we need to follow the rules of algebraic subtraction:
-
Distribute the Negative Sign: The crucial step involves distributing the negative sign (which is implicitly a -1) to each term within the parentheses that are being subtracted. This changes the signs of each term inside those parentheses.
-
Combine Like Terms: After distributing the negative sign, we combine like terms. Like terms are terms that have the same variable raised to the same power. In this case, we have 'x' terms and constant terms.
Let's apply these steps:
(3x - 1) - (3x - 1)
= 3x - 1 - 3x + 1 (Negative sign distributed)
= (3x - 3x) + (-1 + 1) (Like terms grouped)
= 0x + 0 (Like terms combined)
= 0 (Simplified)
Therefore, the answer is 0.
Why the Answer is 0: A Deeper Look
The result of 0 might seem counterintuitive at first. However, it makes perfect sense when considering the nature of subtraction. We're subtracting an identical expression from itself. Think of it like this: if you have five apples and you subtract five apples, you're left with zero apples. The same principle applies here, but with algebraic expressions instead of apples.
The expression 3x - 1 represents a quantity that depends on the value of 'x'. Subtracting the same quantity from itself will always result in zero, regardless of the value of 'x'.
Expanding on Algebraic Subtraction
Let's explore a few more examples to solidify our understanding of algebraic subtraction and its applications:
Example 1: Subtract (2x + 5) from (5x - 2)
(5x - 2) - (2x + 5) = 5x - 2 - 2x - 5 = 3x - 7
Example 2: Subtract (4y² - 3y + 1) from (2y² + 5y - 8)
(2y² + 5y - 8) - (4y² - 3y + 1) = 2y² + 5y - 8 - 4y² + 3y - 1 = -2y² + 8y - 9
Example 3: Subtracting a Monomial from a Polynomial
Subtract 7x from (3x² + 2x - 4)
(3x² + 2x - 4) - 7x = 3x² + 2x - 4 - 7x = 3x² - 5x - 4
These examples highlight the importance of distributing the negative sign correctly and then combining like terms to achieve the simplified result.
Practical Applications of Algebraic Subtraction
Algebraic subtraction isn't just a theoretical exercise; it has numerous practical applications across various fields:
-
Physics and Engineering: Calculating net forces, determining velocity changes, and solving problems related to motion and energy often involve subtracting algebraic expressions.
-
Finance and Economics: Profit calculations, determining net worth, and analyzing financial statements frequently require subtracting expenses from income or assets from liabilities – all involving algebraic subtraction.
-
Computer Science: Writing algorithms, developing software, and managing data structures often rely on the principles of algebraic manipulation, including subtraction.
-
Data Analysis: Subtraction is fundamental in performing statistical analyses, particularly in comparing datasets and identifying differences.
Mastering Algebraic Subtraction: Tips and Tricks
Here are some key tips to master algebraic subtraction:
-
Pay close attention to signs: Distributing the negative sign correctly is crucial to avoid common errors.
-
Group like terms carefully: This step is essential for simplifying the expression efficiently.
-
Practice regularly: Consistent practice is key to mastering any algebraic concept. Work through various examples, including those with multiple variables and more complex expressions.
-
Check your work: After solving a problem, always check your work to ensure the result is correct.
Conclusion: Subtraction's Significance in Algebra
The seemingly simple question, "What is 3x - 1 subtracted from 3x - 1?" reveals a fundamental aspect of algebraic operations: the significance of understanding subtraction as the addition of the opposite. This understanding, combined with the ability to distribute negative signs and combine like terms, forms the bedrock of algebraic manipulation. By mastering these principles, you unlock the ability to tackle more complex algebraic problems and apply this knowledge to diverse real-world applications. The solution, 0, serves as a powerful reminder of the consistent and predictable nature of mathematical operations. The ability to confidently work with algebraic subtraction is crucial for success in numerous academic and professional pursuits.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is -3x+1 Subtracted From 3x-1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.