What Is 4 To The Power Of 6
News Co
Apr 22, 2025 · 5 min read
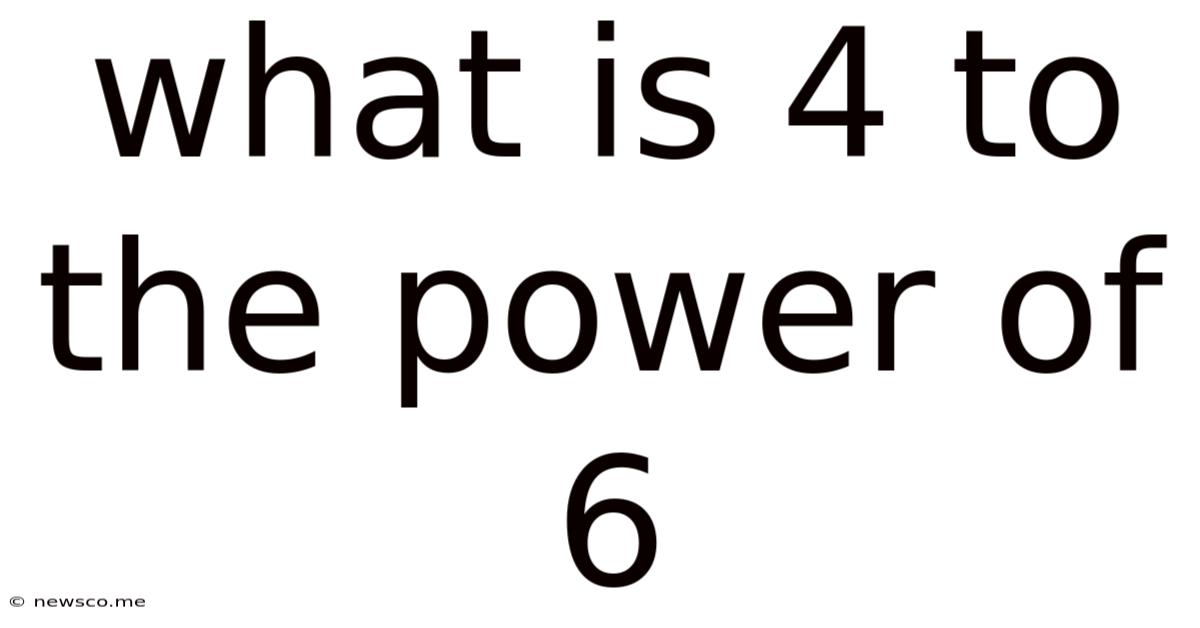
Table of Contents
What is 4 to the Power of 6? A Deep Dive into Exponentiation
The seemingly simple question, "What is 4 to the power of 6?" opens a door to a fascinating world of mathematics, specifically exponentiation. While the answer itself is straightforward to calculate, understanding the underlying concepts and their applications provides a rich learning experience. This article will not only answer the question but also delve into the mechanics of exponentiation, its significance in various fields, and related mathematical concepts.
Understanding Exponentiation
Exponentiation, often represented by a base number raised to an exponent (or power), signifies repeated multiplication. In the expression 4<sup>6</sup>, 4 is the base and 6 is the exponent. This means we multiply 4 by itself six times: 4 × 4 × 4 × 4 × 4 × 4.
Key Terminology:
- Base: The number being multiplied repeatedly (in this case, 4).
- Exponent (or Power): The number indicating how many times the base is multiplied by itself (in this case, 6).
- Result (or Value): The final answer obtained after performing the repeated multiplication.
Calculating 4 to the Power of 6
Let's calculate the value of 4<sup>6</sup> step-by-step:
- 4 × 4 = 16
- 16 × 4 = 64
- 64 × 4 = 256
- 256 × 4 = 1024
- 1024 × 4 = 4096
Therefore, 4 to the power of 6 is 4096.
Beyond the Calculation: Exploring the Implications
While finding the answer is relatively simple, understanding the broader context of exponentiation is crucial. Its applications extend far beyond simple arithmetic.
Exponentiation in Different Fields
1. Computer Science:
Exponentiation is fundamental in computer science, especially in areas like:
- Data Structures: The efficiency of certain data structures, like binary trees, is directly related to exponential growth. Understanding exponential growth helps predict algorithm performance.
- Cryptography: Many encryption algorithms rely heavily on exponentiation with large numbers. The difficulty of calculating the discrete logarithm (finding the exponent given the base and result) is the basis of many secure communication systems.
- Big O Notation: When analyzing algorithm efficiency, Big O notation uses exponential functions (e.g., O(2<sup>n</sup>)) to represent the relationship between input size and execution time. This helps developers choose the most efficient algorithms.
2. Finance:
Compound interest, a cornerstone of finance, utilizes exponentiation. The formula for compound interest involves raising the principal amount to the power of the number of compounding periods. This illustrates the significant impact of compounding over time. Understanding exponential growth allows for accurate prediction of future investment values.
3. Biology:
Exponential growth models are used extensively in biology to describe phenomena like:
- Population Growth: Under ideal conditions, populations of organisms can experience exponential growth. This is represented mathematically using exponential functions.
- Bacterial Growth: The rapid growth of bacterial colonies is often modeled using exponential equations. This knowledge is critical in areas such as epidemiology and medicine.
4. Physics:
Exponentiation appears in various physical phenomena:
- Radioactive Decay: The decay rate of radioactive materials follows an exponential pattern. Understanding this is crucial in areas like nuclear physics and medical imaging.
- Newton's Law of Cooling: This law describes how the temperature of an object changes over time, and the equation often involves exponential terms.
5. Engineering:
Exponential functions are vital in engineering disciplines such as:
- Signal Processing: Analyzing and processing signals, often involving exponential decay or growth, is a cornerstone of signal processing.
- Control Systems: Designing and implementing control systems often requires understanding exponential responses.
Related Mathematical Concepts
Several mathematical concepts are closely related to exponentiation:
1. Logarithms:
Logarithms are the inverse operation of exponentiation. If 4<sup>6</sup> = 4096, then the logarithm base 4 of 4096 is 6 (log<sub>4</sub>(4096) = 6). Logarithms are used to solve equations involving exponents and have numerous applications in various scientific and engineering fields.
2. Roots:
Roots are another related concept. The square root of a number is the value that, when multiplied by itself, gives the original number. Similarly, cube roots, fourth roots, etc., are defined. Roots can be expressed as fractional exponents. For instance, the square root of 4 (√4) can also be written as 4<sup>1/2</sup>.
3. Scientific Notation:
Scientific notation uses exponents to represent very large or very small numbers concisely. This notation is particularly useful in scientific and engineering applications where numbers can span vast ranges.
4. Exponential Functions:
Exponential functions are functions where the variable appears in the exponent. These functions are characterized by their rapid growth or decay. They are frequently used in modeling various phenomena in science, engineering, and finance.
Practical Applications and Problem-Solving
Understanding exponentiation allows us to solve various types of problems. For example:
- Compound Interest Calculations: Determine the future value of an investment after a specified number of years with a given interest rate.
- Population Growth Predictions: Estimate the size of a population after a certain period, given an initial population size and a growth rate.
- Radioactive Decay Estimation: Calculate the amount of a radioactive substance remaining after a specific time, given the initial amount and the half-life.
Advanced Concepts: Complex Numbers and Beyond
While we have focused on real numbers, exponentiation can also be extended to complex numbers. This involves using Euler's formula, a fascinating connection between exponential functions and trigonometric functions. Furthermore, exponentiation can be generalized to other algebraic structures beyond the real and complex numbers, opening up even richer mathematical landscapes.
Conclusion: The Power of Exponentiation
The seemingly simple calculation of 4<sup>6</sup> = 4096 unveils a vast and important area of mathematics with widespread applications across various fields. Understanding exponentiation, its related concepts, and its implications is essential for anyone looking to delve deeper into mathematics, computer science, finance, or any scientific or engineering discipline. From the seemingly mundane to the profoundly complex, exponentiation plays a vital role in shaping our understanding of the world around us. Mastering its concepts unlocks a greater appreciation for the power and elegance of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 4 To The Power Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.