What Is 40 Percent Of 25
News Co
Mar 24, 2025 · 5 min read
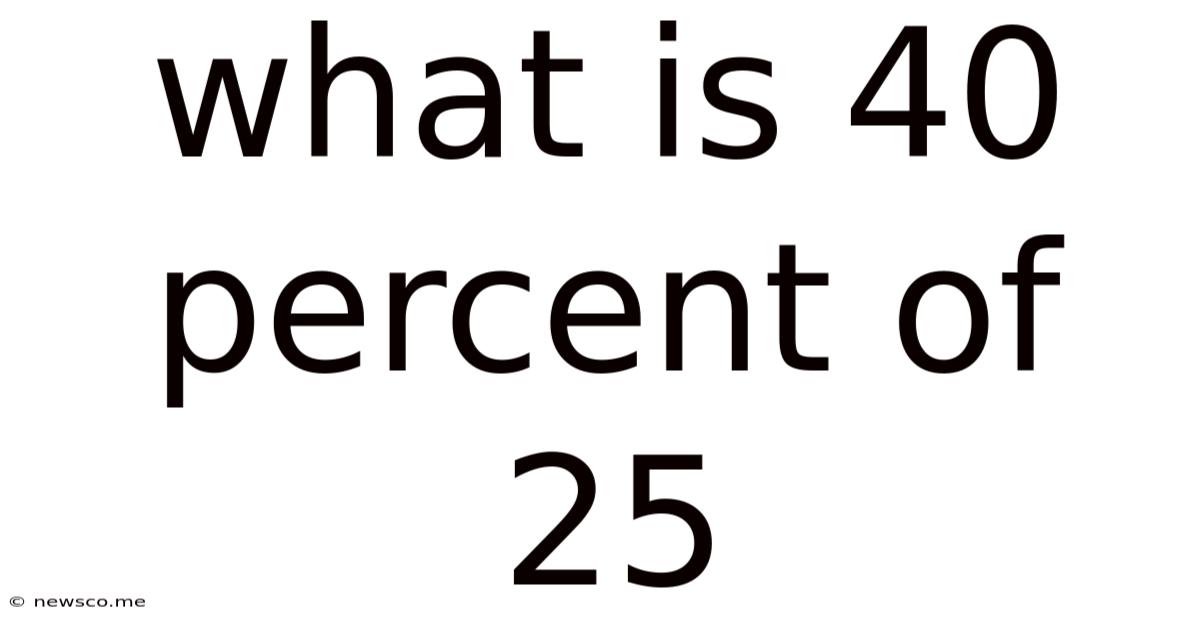
Table of Contents
What is 40 Percent of 25? A Deep Dive into Percentages and Their Applications
Finding 40 percent of 25 might seem like a simple calculation, but it opens a door to understanding a fundamental mathematical concept with far-reaching applications in various fields. This article will not only solve this specific problem but also explore the broader world of percentages, providing you with the tools and knowledge to tackle similar problems with confidence. We'll delve into different methods for calculating percentages, explore real-world examples, and discuss the importance of percentage calculations in various professional and personal contexts.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." Therefore, 40 percent (often written as 40%) means 40 out of 100, or 40/100. This fraction can be simplified to 2/5.
Method 1: Using the Decimal Equivalent
The most straightforward method to calculate 40% of 25 involves converting the percentage to its decimal equivalent. To do this, divide the percentage by 100.
-
Step 1: Convert the percentage to a decimal: 40% ÷ 100 = 0.40
-
Step 2: Multiply the decimal by the number: 0.40 x 25 = 10
Therefore, 40 percent of 25 is $\boxed{10}$.
Method 2: Using Fractions
As mentioned earlier, 40% can be expressed as the fraction 40/100, which simplifies to 2/5. This provides another way to calculate 40% of 25.
-
Step 1: Express the percentage as a fraction: 40% = 40/100 = 2/5
-
Step 2: Multiply the fraction by the number: (2/5) x 25 = (2 x 25) / 5 = 50 / 5 = 10
Again, we arrive at the answer: 40 percent of 25 is $\boxed{10}$.
Method 3: Using Proportions
The concept of percentages can also be approached using proportions. We can set up a proportion to solve for the unknown value (x), which represents 40% of 25.
-
Step 1: Set up the proportion: 40/100 = x/25
-
Step 2: Cross-multiply: 40 x 25 = 100x
-
Step 3: Solve for x: 1000 = 100x => x = 1000/100 = 10
Thus, 40% of 25 is $\boxed{10}$.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in our daily lives, impacting various aspects of personal finance, business, and scientific fields. Let's explore some key applications:
1. Personal Finance:
-
Discounts: Sales and discounts are frequently expressed as percentages. Understanding percentage calculations allows you to quickly determine the final price after a discount. For example, a 20% discount on a $50 item means a saving of $10 (20% of $50).
-
Interest Rates: Interest rates on loans, savings accounts, and credit cards are always expressed as percentages. Calculating interest earned or paid requires a solid understanding of percentage calculations. For example, a 5% interest rate on a $1000 investment would yield $50 in interest in one year (assuming simple interest).
-
Taxes: Sales tax, income tax, and property tax are all calculated as percentages of a certain amount. Knowing how to calculate percentages is crucial for budgeting and financial planning.
-
Tips and Gratuities: Calculating tips in restaurants or service industries involves calculating a percentage of the total bill.
2. Business and Economics:
-
Profit Margins: Businesses use percentage calculations to determine their profit margins, which represent the percentage of revenue remaining after deducting costs.
-
Market Share: Companies track their market share, expressed as a percentage of the total market size.
-
Growth Rates: Economic growth, sales growth, and population growth are often expressed as percentages to show rates of change over time.
-
Inflation: Inflation, the rate at which prices increase, is expressed as a percentage and impacts budgeting and financial decisions.
3. Science and Statistics:
-
Data Analysis: Percentages are frequently used in data analysis and statistics to represent proportions and probabilities. For example, survey results are often presented as percentages to show the distribution of responses.
-
Scientific Experiments: Percentages are used to express the yield of a chemical reaction, the survival rate in a biological experiment, or the accuracy of a measurement.
4. Everyday Life:
-
Recipe Scaling: When adjusting recipes, you often need to scale ingredients up or down by a certain percentage.
-
Surveys and Polls: Understanding percentages is essential for interpreting the results of surveys and polls accurately.
-
Comparing Prices: Comparing prices of different items often involves calculating unit prices and comparing them as percentages.
Beyond the Basics: Compound Interest and More
While our initial problem focused on a simple percentage calculation, understanding percentages extends to more complex scenarios such as compound interest. Compound interest is interest calculated on the initial principal and also on the accumulated interest from previous periods. This leads to exponential growth and is crucial for understanding long-term investments.
Furthermore, percentage change calculations, which measure the relative change between two values, are extensively used in various fields. The formula for percentage change is:
[(New Value - Old Value) / Old Value] x 100%
This allows us to quantify the increase or decrease in a value over time.
Mastering Percentage Calculations: Tips and Tricks
While calculators and software can handle percentage calculations efficiently, a solid understanding of the underlying principles is crucial. Here are some tips and tricks to improve your proficiency:
-
Practice Regularly: Consistent practice is key to mastering any mathematical concept. Work through various examples to build your confidence and speed.
-
Understand the Concepts: Focus on understanding the underlying principles of percentages, rather than just memorizing formulas.
-
Use Different Methods: Try different methods for calculating percentages to find the approach that works best for you.
-
Estimate: Develop the ability to estimate percentages to quickly check your answers and identify potential errors.
-
Use Online Resources: Numerous online resources, including interactive tutorials and practice exercises, are available to enhance your understanding.
Conclusion
In conclusion, while the answer to "What is 40 percent of 25?" is simply 10, the journey to finding this answer has taken us through a fascinating exploration of percentages and their wide-ranging applications. From personal finance to scientific research, the ability to perform percentage calculations efficiently and accurately is a valuable skill with significant implications in various aspects of life. By understanding the different methods, mastering the concepts, and practicing regularly, you can confidently tackle any percentage-related problem and unlock the power of this essential mathematical tool.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 40 Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.