What Is 5/3 As A Percent
News Co
May 08, 2025 · 5 min read
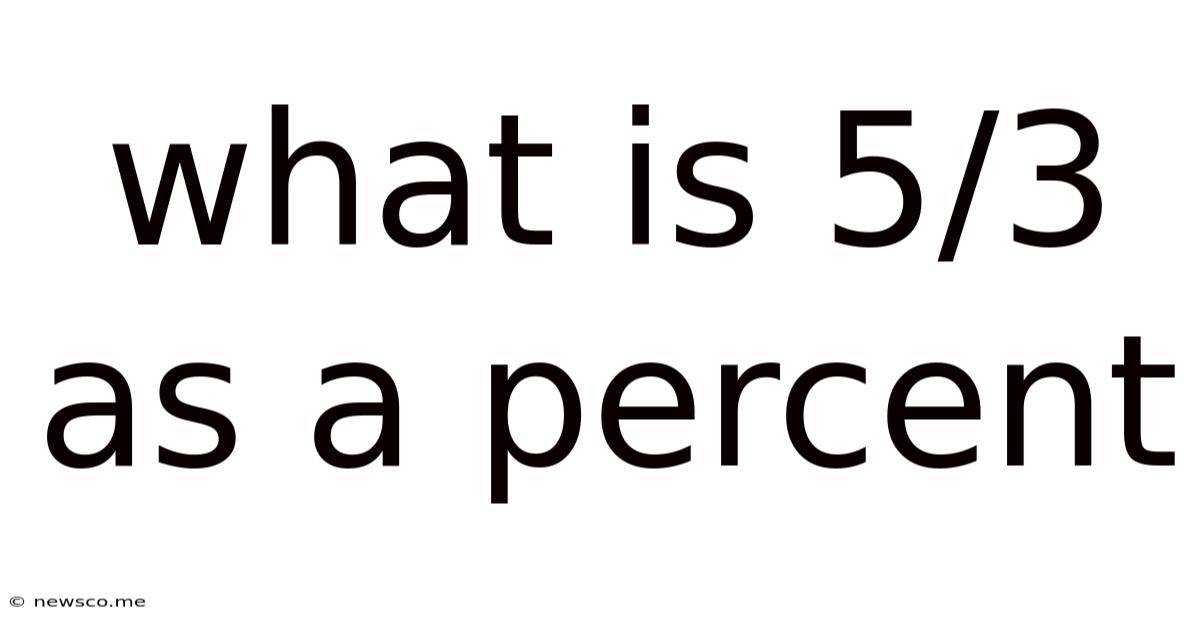
Table of Contents
What is 5/3 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
Converting fractions to percentages is a fundamental skill in mathematics with widespread applications in various fields, from finance and statistics to everyday calculations. This comprehensive guide will delve into the process of converting the fraction 5/3 into a percentage, explaining the underlying concepts and providing practical examples. We'll also explore different methods for performing this conversion and discuss the significance of understanding fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before diving into the conversion, let's refresh our understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts being considered, while the denominator represents the total number of equal parts that make up the whole. In the fraction 5/3, 5 is the numerator and 3 is the denominator. This fraction is an improper fraction because the numerator is larger than the denominator, indicating a value greater than one.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 25% means 25 out of 100, which can also be expressed as the fraction 25/100 or the decimal 0.25.
Converting 5/3 to a Percentage: The Step-by-Step Approach
There are several ways to convert a fraction to a percentage. Let's explore the most common methods:
Method 1: Converting the Fraction to a Decimal, then to a Percentage
-
Divide the numerator by the denominator: To convert 5/3 to a decimal, we divide the numerator (5) by the denominator (3). 5 ÷ 3 = 1.666... (the decimal continues infinitely).
-
Multiply the decimal by 100: To express the decimal as a percentage, we multiply it by 100. 1.666... × 100 = 166.666...%
-
Round to the desired precision: Since the decimal repeats infinitely, we usually round the percentage to a certain number of decimal places. Rounding to two decimal places, we get 166.67%.
Method 2: Direct Conversion using Proportion
This method utilizes the concept of proportionality. We set up a proportion where the fraction 5/3 is equivalent to x/100, where x represents the percentage.
-
Set up the proportion: 5/3 = x/100
-
Cross-multiply: This gives us 3x = 500
-
Solve for x: Divide both sides by 3: x = 500/3 = 166.666...
-
Express as a percentage: Therefore, 5/3 is equal to 166.67% (rounded to two decimal places).
Method 3: Understanding the Whole and the Excess
Since 5/3 is an improper fraction, it represents more than one whole.
-
Determine the number of wholes: 5 divided by 3 is 1 with a remainder of 2. This means 5/3 contains one whole (3/3) and a remaining fraction of 2/3.
-
Convert the remaining fraction to a percentage: 2/3 can be converted to a decimal (2 ÷ 3 ≈ 0.666...) and then to a percentage (0.666... × 100 ≈ 66.67%).
-
Combine the whole and the percentage: One whole is equivalent to 100%, so adding the remaining 66.67% gives us a total of 166.67%.
Practical Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages is crucial in numerous real-world situations:
-
Finance: Calculating interest rates, profit margins, and percentage changes in investments. For example, if a stock price increases by 5/3 of its original value, this translates to a significant 166.67% increase.
-
Statistics: Representing data in percentages for easier understanding and comparison. For instance, if a survey shows that 5 out of 3 respondents prefer a particular product, this translates to a strong 166.67% preference rate, suggesting a significant majority.
-
Everyday life: Calculating discounts, tips, and sales tax. For instance, a 5/3 increase in the price of a product represents a 166.67% markup.
-
Science and Engineering: Expressing ratios and proportions in percentage terms. For example, if the output of a machine is 5/3 times its input, this corresponds to a 166.67% increase in productivity.
Advanced Considerations: Working with Mixed Numbers and Decimal Fractions
While our example focuses on an improper fraction, it's also beneficial to understand how to convert mixed numbers and fractions with decimal components to percentages.
Mixed Numbers: A mixed number combines a whole number and a fraction (e.g., 1 2/3). To convert a mixed number to a percentage, first convert it into an improper fraction, then follow the steps outlined earlier. For example, 1 2/3 = 5/3, which we've already shown to be 166.67%.
Decimal Fractions: If the fraction contains decimal components (e.g., 5.2/3), perform the division as usual (5.2 ÷ 3 ≈ 1.7333...) and then multiply by 100 to convert the decimal to a percentage (1.7333... × 100 ≈ 173.33%).
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a vital mathematical skill applicable across diverse fields. The ability to seamlessly transition between fractions and percentages enhances numerical fluency and allows for efficient data interpretation and analysis. Understanding the different methods for performing this conversion—whether through direct decimal conversion or by utilizing proportional reasoning—provides a robust toolkit for tackling real-world problems involving fractions and percentages. Remember to always round appropriately based on the context and desired precision. Mastering this skill will undoubtedly enhance your problem-solving capabilities and improve your understanding of numerical relationships.
Latest Posts
Latest Posts
-
Volume Of Rectangular Prism With Half Cylinder
May 08, 2025
-
Cuanto Es 40 Grados En Estados Unidos
May 08, 2025
-
What Is The Lcm For 5 6 7
May 08, 2025
-
Differentiate To The Power Of X
May 08, 2025
-
How Much Is 12000 Pounds In American Money
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 5/3 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.