What Is 5 8 Of 1 2
News Co
Apr 10, 2025 · 5 min read
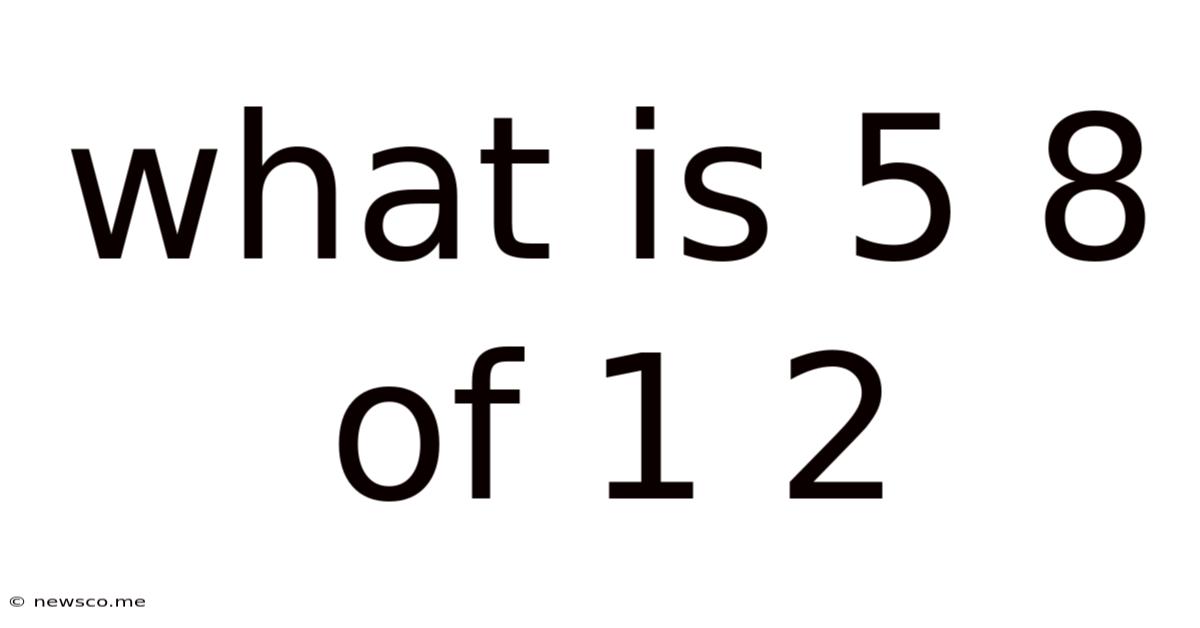
Table of Contents
What is 5/8 of 1/2? A Deep Dive into Fractions and Their Applications
This seemingly simple question, "What is 5/8 of 1/2?", opens a door to a fascinating world of fractions, their manipulation, and their widespread applications in various fields. Understanding how to solve this problem isn't just about getting the right answer; it's about grasping fundamental mathematical concepts that are crucial for everything from baking a cake to designing a skyscraper. This article will delve into the solution, explore the underlying principles, and showcase the real-world relevance of fractional calculations.
Understanding Fractions: The Building Blocks
Before tackling the problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating how many equal parts the whole is divided into.
For example, in the fraction 1/2 (one-half), the numerator is 1, and the denominator is 2. This signifies that we have one part out of two equal parts that make up the whole.
Solving "What is 5/8 of 1/2?"
The phrase "of" in mathematics generally implies multiplication. Therefore, to find 5/8 of 1/2, we need to multiply the two fractions:
(5/8) * (1/2)
To multiply fractions, we multiply the numerators together and the denominators together:
(5 * 1) / (8 * 2) = 5/16
Therefore, 5/8 of 1/2 is 5/16.
Beyond the Calculation: Exploring the Concepts
While the calculation itself is straightforward, the underlying concepts deserve further exploration:
1. Visualizing Fractions
Visual aids can significantly improve understanding. Imagine a rectangular cake. To represent 1/2, we cut the cake into two equal pieces and take one. To find 5/8 of this 1/2, we would need to further divide that half-cake into eight equal slices and take five of them. The resulting portion represents 5/16 of the original whole cake.
2. Equivalent Fractions
Understanding equivalent fractions is vital. A fraction can have many equivalent representations. For example, 1/2 is equivalent to 2/4, 3/6, 4/8, and so on. These fractions all represent the same amount, just expressed differently. This concept is useful for simplifying fractions and performing calculations.
3. Simplifying Fractions
Simplifying a fraction means reducing it to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. In the case of 5/16, the GCD of 5 and 16 is 1. Since they share no common factors other than 1, the fraction is already in its simplest form.
4. Improper Fractions and Mixed Numbers
Sometimes, the result of a fraction calculation might be an improper fraction – where the numerator is larger than the denominator (e.g., 7/4). These can be converted into mixed numbers, which combine a whole number and a proper fraction (e.g., 1 3/4). While 5/16 is a proper fraction, understanding this conversion is crucial for more complex calculations.
Real-World Applications of Fractional Calculations
Fractions are not just abstract mathematical concepts; they have countless practical applications across various fields:
1. Cooking and Baking
Recipes frequently involve fractions. Understanding how to accurately measure ingredients, like 1/4 cup of sugar or 2/3 cup of flour, is essential for successful cooking and baking. Calculating the correct proportions when scaling recipes up or down also relies heavily on fractional calculations.
2. Construction and Engineering
Engineers and architects use fractions extensively in their designs. Precise measurements and calculations are critical, and fractions often help in dealing with precise dimensions and material quantities. For example, blueprint designs will frequently use fractional measurements in inches or centimeters.
3. Finance and Budgeting
Fractions are fundamental to understanding financial concepts like interest rates, discounts, and proportions of budgets. Calculating interest on loans, determining the percentage of a discount, or dividing a budget across different categories all involve working with fractions and percentages (which are essentially fractions expressed as a portion of 100).
4. Science and Medicine
Fractions are integral to scientific measurements and experiments. Scientists may use fractions to express concentrations of solutions, proportions in chemical reactions, or to represent data points on graphs and charts. In medicine, doses of medication are often described using fractions, emphasizing the importance of precision in dosage calculations.
5. Everyday Life
Beyond these specialized fields, fractions pop up in everyday scenarios. Sharing items equally among friends, measuring ingredients for a simple recipe, or understanding sale discounts all involve fractional calculations, often unconsciously.
Mastering Fractions: Tips and Resources
Developing a strong understanding of fractions is crucial for academic success and practical life. Here are some tips for improving your fractional skills:
- Practice regularly: The more you practice, the more comfortable you will become with various fractional operations.
- Visualize problems: Use diagrams and visual representations to understand concepts more clearly.
- Use online resources: Numerous websites and apps offer interactive lessons and practice exercises on fractions.
- Seek help when needed: Don't hesitate to ask for help from teachers, tutors, or friends if you're struggling with a particular concept.
Conclusion: The Importance of Understanding Fractions
This in-depth exploration of the seemingly simple question "What is 5/8 of 1/2?" has illuminated the fundamental role of fractions in mathematics and their far-reaching applications in the real world. Mastering fractional calculations is not merely an academic exercise; it's a key skill that empowers you to approach numerous problems and challenges across various disciplines with confidence and accuracy. From scaling recipes to designing bridges, fractions are a cornerstone of quantitative reasoning, making their understanding essential for success in many aspects of life. So, the next time you encounter a fraction, remember the power and practicality it holds.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 5 8 Of 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.