What Is 5 Out Of 8 As A Percentage
News Co
Mar 21, 2025 · 4 min read
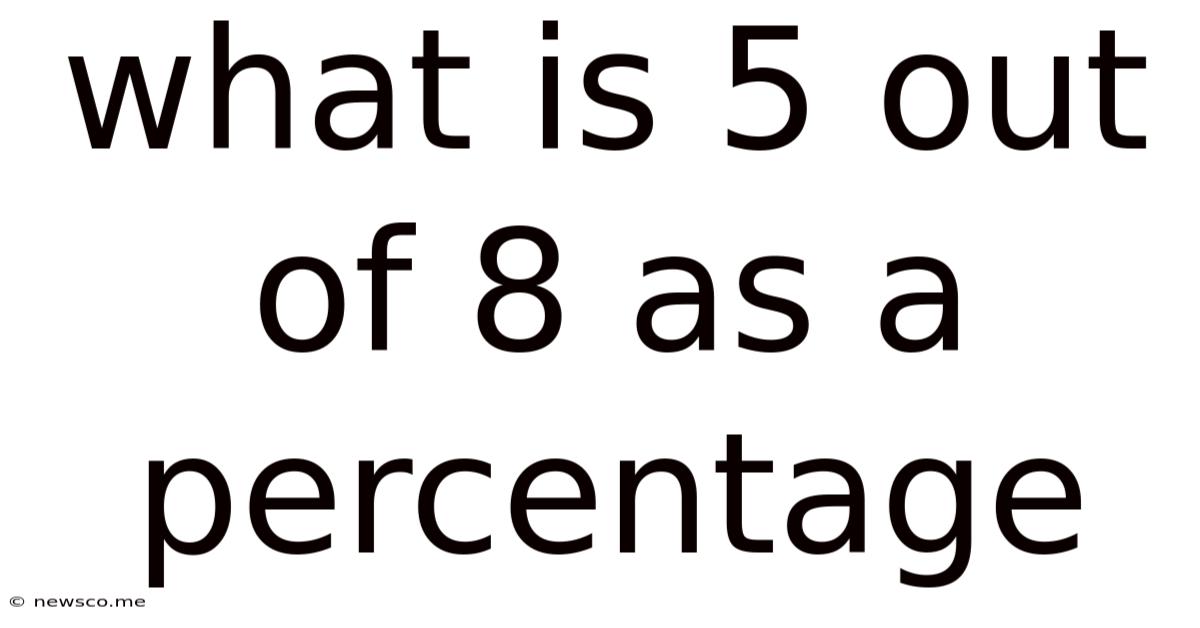
Table of Contents
What is 5 out of 8 as a Percentage? A Comprehensive Guide
Determining percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex scientific calculations. Understanding how to convert fractions into percentages is crucial for accurate analysis and informed decision-making. This comprehensive guide will delve into the calculation of "5 out of 8 as a percentage," explaining the process step-by-step and exploring related concepts to solidify your understanding.
Understanding Fractions and Percentages
Before tackling the specific problem, let's clarify the underlying concepts. A fraction represents a part of a whole. In the case of "5 out of 8," 5 represents the part, and 8 represents the whole. This can be written as 5/8.
A percentage, denoted by the symbol %, signifies a fraction out of 100. It provides a standardized way to compare and understand proportions. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating 5 out of 8 as a Percentage: The Step-by-Step Approach
To convert the fraction 5/8 into a percentage, we need to express it as a fraction with a denominator of 100. Here's how:
Step 1: Divide the numerator by the denominator.
Divide 5 (the numerator) by 8 (the denominator):
5 ÷ 8 = 0.625
Step 2: Multiply the result by 100.
Multiply the decimal obtained in Step 1 by 100 to convert it into a percentage:
0.625 × 100 = 62.5
Step 3: Add the percentage symbol.
Finally, add the percentage symbol (%) to indicate that the result is a percentage:
62.5%
Therefore, 5 out of 8 is equal to 62.5%.
Alternative Methods for Calculating Percentages
While the above method is straightforward, there are alternative approaches you can use to calculate percentages. These methods can be helpful depending on the complexity of the fraction or your personal preference.
Method 1: Using Proportions
You can set up a proportion to solve for the percentage:
5/8 = x/100
Cross-multiply:
8x = 500
Solve for x:
x = 500/8 = 62.5
Therefore, x = 62.5%, confirming our earlier result.
Method 2: Using a Calculator
Most calculators have a percentage function. Simply enter 5 ÷ 8 and then multiply by 100 to obtain the percentage directly. This method is particularly efficient for more complex fractions.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages has numerous practical applications in various aspects of life:
Finance and Budgeting:
- Calculating discounts: If a store offers a 20% discount on an item, you can easily determine the discounted price by calculating the percentage of the original price.
- Understanding interest rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Calculating these percentages is crucial for financial planning.
- Analyzing financial statements: Financial reports often utilize percentages to represent key financial metrics, allowing for easier comparison and analysis across different periods or entities.
Science and Statistics:
- Expressing experimental results: Scientific experiments often involve calculating percentages to represent the success rate or the proportion of a specific outcome.
- Analyzing statistical data: Percentages are fundamental in presenting and interpreting statistical data, helping to visualize and understand trends and patterns.
Everyday Life:
- Calculating tips: When dining out, you can use percentages to calculate a gratuity based on the total bill amount.
- Understanding survey results: Surveys often present results as percentages, making it easier to understand public opinion or preferences.
- Tracking progress: You can use percentages to track progress towards a goal, whether it's completing a project, achieving a fitness target, or saving money.
Expanding Your Understanding: Working with Different Fractions
The principles discussed above apply to any fraction. Let's explore a few more examples to reinforce your understanding:
Example 1: What is 3 out of 5 as a percentage?
- 3 ÷ 5 = 0.6
- 0.6 × 100 = 60
- Therefore, 3 out of 5 is 60%.
Example 2: What is 12 out of 20 as a percentage?
- 12 ÷ 20 = 0.6
- 0.6 × 100 = 60
- Therefore, 12 out of 20 is 60%. Notice that this simplifies to 3/5, the same as the previous example.
Example 3: What is 7 out of 15 as a percentage?
- 7 ÷ 15 ≈ 0.4667
- 0.4667 × 100 ≈ 46.67
- Therefore, 7 out of 15 is approximately 46.67%.
Dealing with Decimals and Complex Fractions
The process remains the same even when dealing with decimals or complex fractions. The key is to maintain accuracy in your calculations.
Example: What is 2.5 out of 10 as a percentage?
- 2.5 ÷ 10 = 0.25
- 0.25 × 100 = 25
- Therefore, 2.5 out of 10 is 25%.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill that enhances your ability to interpret data, make informed decisions, and solve problems across various domains. By understanding the fundamental principles and practicing different methods, you can confidently tackle any percentage calculation, from simple fractions to more complex scenarios. Remember the core steps: divide the numerator by the denominator, multiply by 100, and add the percentage symbol. This straightforward approach provides a reliable and efficient way to convert fractions into percentages. With consistent practice, you'll find yourself effortlessly navigating the world of percentages and applying this crucial skill to your daily life and professional endeavors.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 5 Out Of 8 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.