What Is 5 Percent Of 200
News Co
Mar 23, 2025 · 6 min read
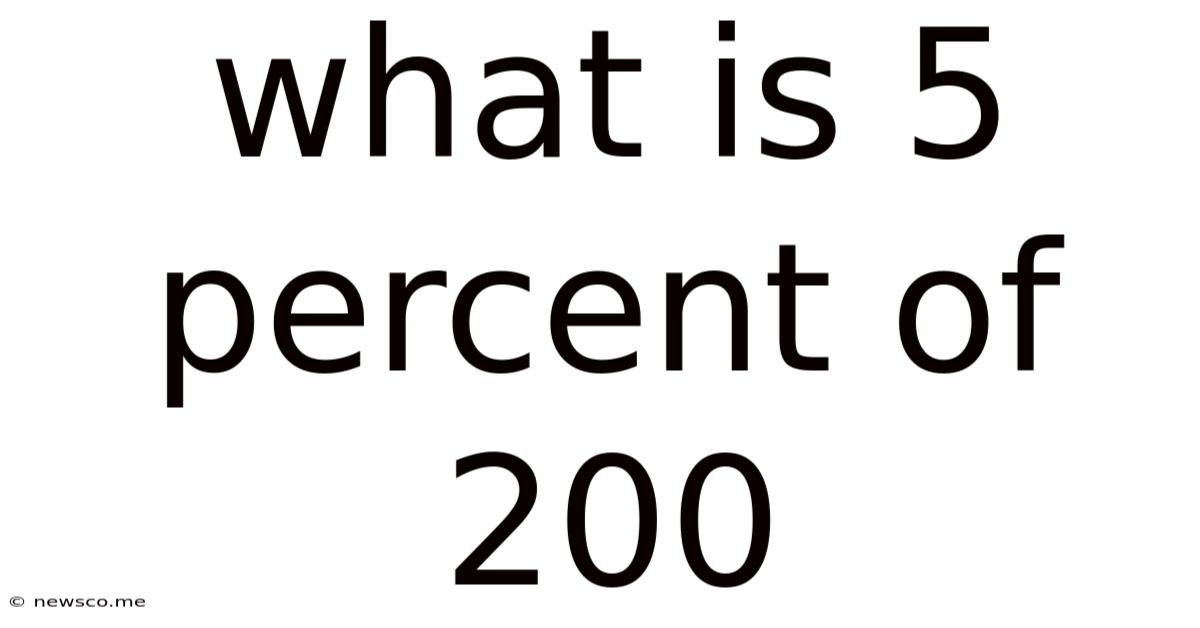
Table of Contents
What is 5 Percent of 200? A Deep Dive into Percentages and Their Applications
Finding 5 percent of 200 might seem like a simple calculation, easily solved with a calculator. However, understanding the underlying principles of percentages and their widespread applications is crucial in various aspects of life, from everyday finances to complex statistical analyses. This article will not only answer the question directly but also explore the broader concept of percentages, demonstrating their importance and providing practical examples.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." This implies that a percentage represents a proportion of a whole. For instance, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5.
Key Concepts Related to Percentages:
-
Percentage Calculation: The basic formula for calculating a percentage is: (Part / Whole) * 100 = Percentage. This formula allows us to determine the percentage that one quantity represents of another.
-
Finding a Percentage of a Number: To find a percentage of a number, we multiply the number by the percentage expressed as a decimal. For example, to find 10% of 200, we calculate 200 * 0.10 = 20.
-
Converting Percentages to Decimals and Fractions: Converting between percentages, decimals, and fractions is crucial for calculations. To convert a percentage to a decimal, divide by 100 (move the decimal point two places to the left). To convert a decimal to a percentage, multiply by 100 (move the decimal point two places to the right). To convert a percentage to a fraction, write the percentage as a fraction with a denominator of 100 and simplify.
Calculating 5 Percent of 200
Now, let's tackle the central question: What is 5 percent of 200?
We can use the formula mentioned earlier:
(Part / Whole) * 100 = Percentage
In this case, we know the whole (200) and the percentage (5%). We need to find the part. We can rearrange the formula to solve for the part:
Part = (Percentage / 100) * Whole
Substituting the values:
Part = (5 / 100) * 200
Part = 0.05 * 200
Part = 10
Therefore, 5 percent of 200 is 10.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world scenarios:
1. Finance and Budgeting:
-
Interest Rates: Understanding interest rates, whether on loans, savings accounts, or investments, requires percentage calculations. For example, calculating the interest earned on a savings account or the total amount payable on a loan with compound interest.
-
Discounts and Sales Tax: Calculating discounts offered during sales or adding sales tax to a purchase price involves percentage calculations. For example, figuring out the final price after a 20% discount or the total cost including 6% sales tax.
-
Investment Returns: Investors use percentage calculations to track the returns on their investments, comparing performance across different asset classes. Understanding percentage changes in investment values is vital for making informed decisions.
-
Budget Allocation: Individuals and organizations use percentages to allocate their budgets effectively, deciding how much to spend on different categories like housing, food, transportation, and entertainment.
2. Statistics and Data Analysis:
-
Descriptive Statistics: Percentages are frequently used in descriptive statistics to summarize data. For example, expressing the proportion of a population with a specific characteristic, like the percentage of voters who support a particular candidate.
-
Inferential Statistics: Percentages play a key role in inferential statistics, helping researchers to make inferences about populations based on sample data. Confidence intervals and hypothesis testing often involve percentage calculations.
-
Data Visualization: Charts and graphs often use percentages to represent data visually, making complex information easier to understand. Pie charts, bar graphs, and line graphs frequently utilize percentages.
3. Everyday Life:
-
Tipping in Restaurants: Calculating a tip at a restaurant typically involves determining a percentage of the bill amount. For example, a 15% or 20% tip on a meal.
-
Grading Systems: Many educational systems use percentages to represent grades and scores, allowing for easy comparison of student performance.
-
Sales and Commissions: Salespeople often earn commissions based on a percentage of their sales, making percentage calculations essential for determining their income.
-
Recipe Scaling: Adjusting recipe quantities involves percentage calculations, especially when increasing or decreasing the serving size. For instance, if a recipe serves four and you want to double it, you would increase each ingredient by 50%.
4. Science and Engineering:
-
Concentration of Solutions: In chemistry, percentages are used to express the concentration of a solution, such as the percentage of solute in a solvent.
-
Efficiency and Performance: In engineering, percentages are used to represent efficiency and performance metrics for various systems and machines.
-
Error Rates: In many scientific experiments, percentage errors are calculated to assess the accuracy of measurements and results.
Beyond the Basics: More Complex Percentage Calculations
While calculating 5% of 200 is straightforward, more complex scenarios may require multiple steps. For instance:
-
Finding the original amount after a percentage increase or decrease: If an item's price increased by 10% to $220, to find the original price, you would divide $220 by 1.10 (1 + 0.10).
-
Calculating percentage change: To determine the percentage change between two values, calculate the difference between the two values, divide by the original value, and multiply by 100.
-
Compounding percentages: When percentages are applied repeatedly, like with compound interest, the calculations become more intricate, involving exponential growth or decay.
Mastering Percentages: Tips and Tricks
To improve your proficiency with percentage calculations:
-
Practice Regularly: Consistent practice is key to mastering percentage calculations. Start with simple problems and gradually increase the complexity.
-
Use a Calculator: Don't hesitate to use a calculator for more complex calculations. Calculators can handle large numbers and decimal places efficiently.
-
Understand the Underlying Concepts: Focus on understanding the underlying principles of percentages, decimals, and fractions, which will help you solve a wide range of percentage problems.
-
Utilize Online Resources: Numerous online resources, including websites and tutorials, provide explanations, practice problems, and interactive exercises to help you improve your understanding of percentages.
-
Break Down Complex Problems: When faced with a complex percentage problem, break it down into smaller, more manageable steps. This will help you avoid errors and understand the solution process more clearly.
Conclusion
Calculating 5 percent of 200, while seemingly simple, provides a springboard to understanding the broader concept of percentages and their vast applications. From managing personal finances to analyzing complex datasets, the ability to calculate and interpret percentages is a fundamental skill with implications across numerous fields. Mastering this skill empowers you to make informed decisions, solve real-world problems, and navigate the complexities of numerical data effectively. By understanding the principles and practicing regularly, you can confidently tackle any percentage-related challenge that comes your way.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 5 Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.