What Is 5 Percent Of 60
News Co
Apr 15, 2025 · 5 min read
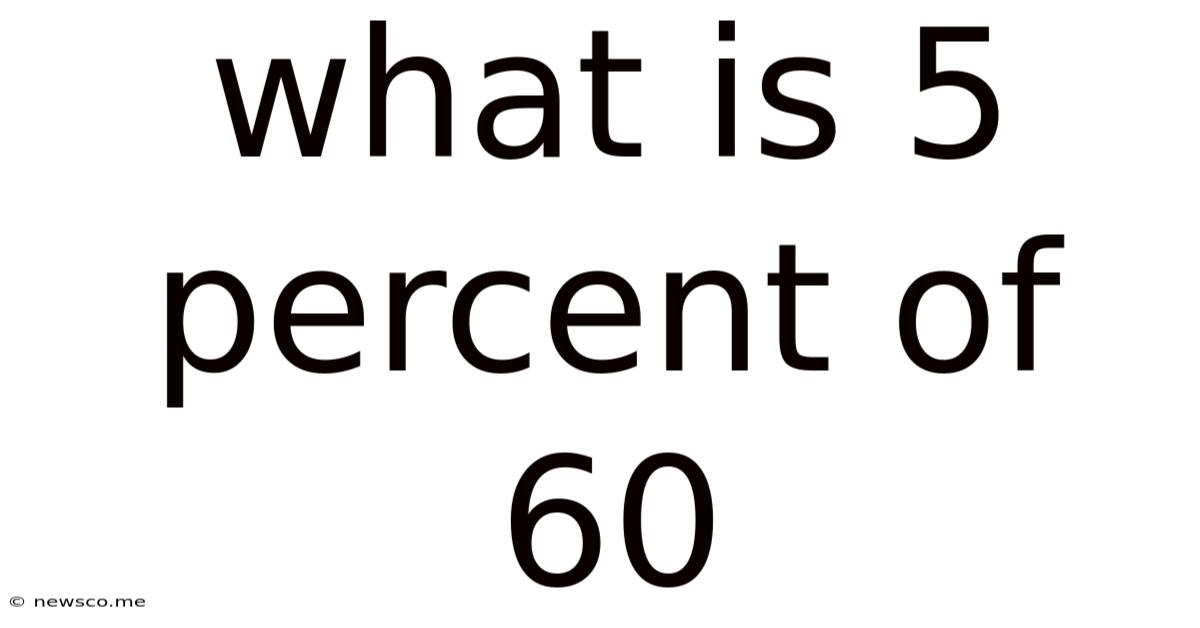
Table of Contents
What is 5 Percent of 60? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from finance and budgeting to sales and statistics. Understanding how to determine a percentage of a number is crucial for everyday life and professional success. This article will comprehensively explore the question, "What is 5 percent of 60?", providing not just the answer but also a detailed explanation of the process, variations, and practical applications.
Understanding Percentages
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is a fraction expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 5% can be written as 5/100 or 0.05. This decimal representation is key to performing percentage calculations efficiently.
Calculating 5 Percent of 60: The Three Main Methods
There are three primary methods to calculate 5% of 60:
Method 1: Using the Decimal Form
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the number.
- Convert the percentage to a decimal: 5% = 5/100 = 0.05
- Multiply the decimal by the number: 0.05 * 60 = 3
Therefore, 5% of 60 is $\boxed{3}$.
Method 2: Using the Fraction Form
This method involves converting the percentage to a fraction and then performing the multiplication.
- Convert the percentage to a fraction: 5% = 5/100
- Simplify the fraction (optional): 5/100 simplifies to 1/20
- Multiply the fraction by the number: (1/20) * 60 = 60/20 = 3
Again, we arrive at the answer: 5% of 60 is $\boxed{3}$.
Method 3: Using the Proportion Method
This method uses proportions to solve for the unknown value. We set up a proportion where one ratio represents the percentage and the other represents the part of the whole.
- Set up the proportion: 5/100 = x/60, where 'x' represents 5% of 60.
- Cross-multiply: 100x = 5 * 60
- Solve for x: 100x = 300 => x = 300/100 = 3
This method confirms that 5% of 60 is $\boxed{3}$.
Practical Applications of Percentage Calculations
The ability to calculate percentages has wide-ranging applications in various aspects of life:
1. Finance and Budgeting:
- Calculating interest: Understanding percentages is crucial for calculating simple and compound interest on loans, savings accounts, and investments. For example, calculating the interest earned on a savings account or the interest paid on a loan requires precise percentage calculations.
- Sales tax: Determining the sales tax on a purchase involves calculating a percentage of the original price.
- Discounts: Calculating the discount on an item during a sale requires calculating a percentage of the original price. For example, a 20% discount on a $100 item would be a savings of $20.
- Tips: Calculating the appropriate tip in a restaurant often involves determining a percentage of the total bill. A common tip percentage is 15% or 20%.
- Budgeting: Allocating funds for different categories in a budget involves expressing expenses as a percentage of total income. For instance, allocating 30% of income for housing expenses.
2. Sales and Marketing:
- Commission: Calculating sales commissions based on a percentage of sales revenue.
- Market share: Analyzing the market share of a company or product requires expressing it as a percentage of the total market.
- Conversion rates: Tracking the conversion rate of online marketing campaigns involves calculating the percentage of visitors who complete a desired action (e.g., making a purchase).
- Profit margins: Determining the profit margin on a product or service necessitates calculating the percentage of profit relative to the cost.
3. Statistics and Data Analysis:
- Probability: Expressing the likelihood of an event occurring as a percentage.
- Data representation: Using percentages to visually represent data in graphs and charts (e.g., pie charts).
- Growth rates: Calculating the percentage growth or decline of a variable over time (e.g., population growth, sales growth).
4. Everyday Life:
- Cooking: Following recipes often involves adjusting ingredient quantities based on percentages.
- Shopping: Comparing prices and discounts across different stores requires a good understanding of percentages.
- Understanding data: Interpreting statistics presented as percentages in news articles or reports.
Beyond the Basics: Working with More Complex Percentage Problems
While calculating 5% of 60 is a relatively simple problem, the fundamental principles can be applied to more complex scenarios. Let's explore some examples:
- Finding the original amount: If you know that 15% of a number is 9, you can use the same principles to work backward and find the original number. Set up the equation: 0.15x = 9. Solving for x (the original number) gives you 60.
- Calculating percentage increase/decrease: Finding the percentage increase or decrease between two numbers involves calculating the difference between the two numbers, dividing by the original number, and multiplying by 100%.
- Calculating percentages of multiple numbers: You can apply these principles to calculate percentages of multiple numbers sequentially, adding or subtracting the results to obtain a final percentage.
Conclusion: Mastering Percentages for a More Informed Life
Understanding percentage calculations is an essential skill applicable in various facets of life. Mastering this skill equips you with the tools to analyze data, make informed financial decisions, understand marketing strategies, and interpret statistical information effectively. This article has explored the various methods for calculating percentages, highlighting the practical applications of this fundamental mathematical concept. By solidifying your understanding of percentages, you'll enhance your ability to navigate the complexities of the modern world with confidence and precision. Remember, even seemingly simple calculations like "What is 5 percent of 60?" form the building blocks of more complex numerical reasoning.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 5 Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.