What Is 5 To The 4 Power
News Co
Mar 26, 2025 · 6 min read
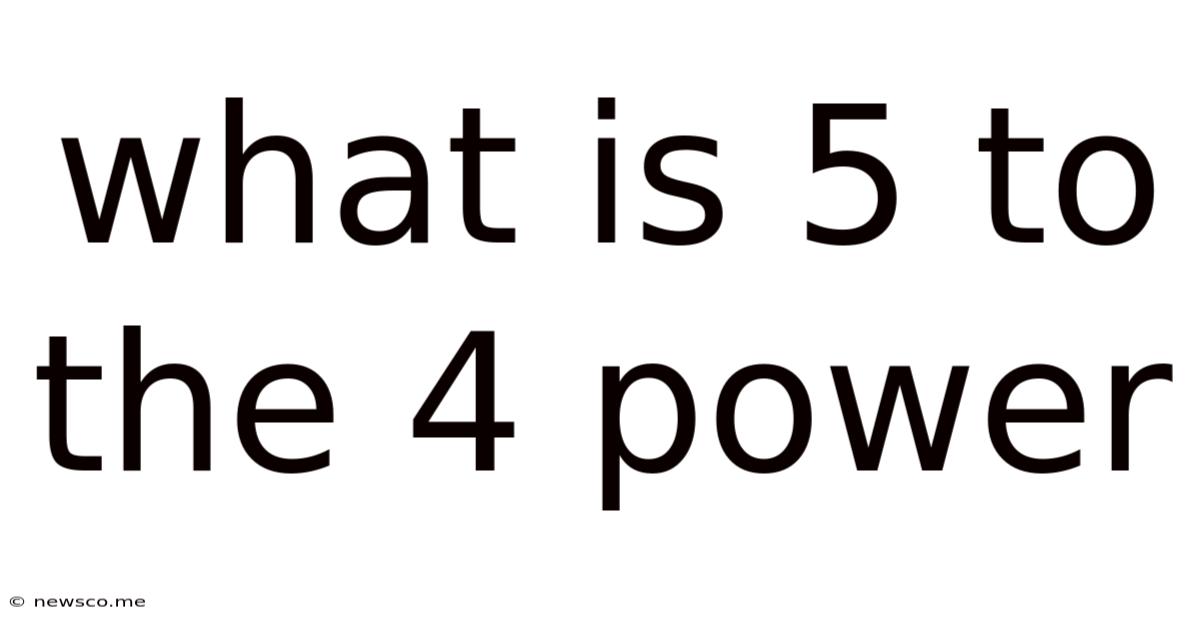
Table of Contents
What is 5 to the 4th Power? A Deep Dive into Exponents and Their Applications
Understanding exponents is fundamental to mathematics and numerous scientific fields. This article delves into the meaning of "5 to the 4th power" (often written as 5⁴), exploring its calculation, practical applications, and the broader concept of exponential notation. We'll also examine related concepts and explore how understanding exponents can help you excel in various areas.
Decoding the Exponent: What Does 5⁴ Mean?
In mathematics, an exponent (also called a power or index) indicates how many times a number (the base) is multiplied by itself. In the expression 5⁴, '5' is the base, and '4' is the exponent. This means we multiply 5 by itself four times:
5⁴ = 5 * 5 * 5 * 5 = 625
Therefore, 5 to the 4th power is equal to 625. This seemingly simple calculation forms the basis for understanding more complex mathematical operations and concepts.
Understanding Exponents: Beyond the Basics
The concept of exponents extends far beyond simple calculations like 5⁴. Let's explore some key aspects:
Different Exponents: Exploring the Landscape
- Exponent of 0: Any non-zero number raised to the power of 0 equals 1. For example, 5⁰ = 1.
- Exponent of 1: Any number raised to the power of 1 equals itself. For example, 5¹ = 5.
- Negative Exponents: A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example, 5⁻² = 1/5² = 1/25.
- Fractional Exponents: Fractional exponents represent roots. For example, 5^(1/2) is the square root of 5, and 5^(1/3) is the cube root of 5.
- Large Exponents: As the exponent increases, the value of the expression grows rapidly. This rapid growth is characteristic of exponential functions and is central to many real-world phenomena.
The Power of Exponential Growth
Exponential growth describes situations where a quantity increases by a fixed percentage over time. The growth isn't linear; it accelerates dramatically. Examples include:
- Population Growth: The population of a species can exhibit exponential growth under ideal conditions.
- Compound Interest: The interest earned on an investment grows exponentially when interest is compounded.
- Viral Spread: The spread of a virus or an online trend can be modeled using exponential functions.
- Radioactive Decay: The decay of radioactive materials follows an exponential pattern.
Working with Exponents: Key Rules and Properties
Several rules govern how we work with exponents. Mastering these rules is crucial for more advanced mathematical operations:
- Product Rule: When multiplying numbers with the same base, add the exponents: aᵐ * aⁿ = a^(m+n)
- Quotient Rule: When dividing numbers with the same base, subtract the exponents: aᵐ / aⁿ = a^(m-n)
- Power Rule: When raising a power to another power, multiply the exponents: (aᵐ)ⁿ = a^(m*n)
- Power of a Product Rule: When raising a product to a power, raise each factor to that power: (ab)ⁿ = aⁿbⁿ
- Power of a Quotient Rule: When raising a quotient to a power, raise both the numerator and the denominator to that power: (a/b)ⁿ = aⁿ/bⁿ
Practical Applications of Exponents: Real-World Examples
Exponents are not just abstract mathematical concepts; they have wide-ranging practical applications across numerous fields:
Science and Engineering
- Physics: Exponents are fundamental to describing physical phenomena, such as the inverse square law (e.g., the intensity of light decreases with the square of the distance).
- Chemistry: Exponents are crucial in stoichiometry (calculations involving chemical reactions) and in describing the rates of chemical reactions.
- Engineering: Exponents are used in calculations related to structural design, electrical circuits, and many other engineering disciplines.
Finance and Economics
- Compound Interest: As mentioned earlier, compound interest calculations rely heavily on exponents. Understanding exponential growth is crucial for financial planning and investment strategies.
- Economic Modeling: Exponential functions are used in economic models to describe growth and decay processes, such as GDP growth or inflation rates.
Computer Science
- Big O Notation: Exponents are used in Big O notation to describe the efficiency of algorithms. This helps computer scientists analyze the performance of their code.
- Data Structures: The size and efficiency of certain data structures, like binary trees, are related to exponential functions.
Biology and Medicine
- Population Dynamics: Exponential growth and decay models are essential in understanding population dynamics in various species.
- Pharmacokinetics: Exponents are used in describing how drugs are absorbed, distributed, metabolized, and excreted by the body.
Beyond 5⁴: Exploring Exponential Functions
The concept of 5⁴ extends to the broader realm of exponential functions. An exponential function is a function of the form f(x) = aˣ, where 'a' is a constant (the base) and 'x' is the exponent (the variable). The graph of an exponential function shows the characteristic rapid growth or decay.
Exponential Growth vs. Exponential Decay
- Exponential Growth: When the base 'a' is greater than 1, the function represents exponential growth. The value of the function increases rapidly as x increases.
- Exponential Decay: When the base 'a' is between 0 and 1, the function represents exponential decay. The value of the function decreases rapidly as x increases.
Applications of Exponential Functions
Exponential functions are used extensively to model phenomena exhibiting rapid growth or decay, including:
- Radioactive decay: The amount of a radioactive substance remaining after a certain time can be modeled using an exponential decay function.
- Population growth (with limitations): Logistic growth models incorporate both exponential growth and limiting factors to more realistically represent population dynamics.
- Cooling of objects: Newton's Law of Cooling uses exponential functions to describe how the temperature of an object changes over time.
Mastering Exponents: Tips and Resources
To truly master exponents and their applications, consider these strategies:
- Practice Regularly: Consistent practice is key to developing a strong understanding of exponent rules and their applications. Work through a variety of problems, starting with simple calculations and progressing to more complex ones.
- Use Visual Aids: Graphs and diagrams can help visualize exponential growth and decay, making the concepts easier to understand.
- Seek Additional Resources: Numerous online resources, textbooks, and educational videos are available to enhance your understanding of exponents.
- Connect with Others: Discuss concepts with fellow students or teachers to solidify your understanding and gain different perspectives.
Conclusion: The Enduring Significance of Exponents
From basic calculations like 5⁴ to complex mathematical models, exponents play a crucial role in numerous fields. Understanding exponents is not just about performing calculations; it's about grasping the fundamental principles of exponential growth and decay, which govern many processes in the natural world and human endeavors. By mastering exponents and related concepts, you open doors to deeper understanding and broader applications across various disciplines. The seemingly simple calculation of 5⁴ serves as a gateway to a vast and fascinating world of mathematics and its applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 5 To The 4 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.