What Is 5 To The Fifth Power
News Co
Apr 05, 2025 · 5 min read
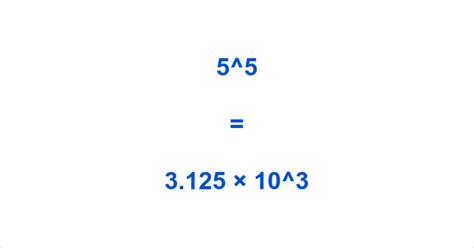
Table of Contents
What is 5 to the Fifth Power? A Deep Dive into Exponentiation
The seemingly simple question, "What is 5 to the fifth power?" opens a door to a fascinating world of mathematics, specifically exponentiation. Understanding this concept not only provides the answer to this specific question but also lays the groundwork for tackling more complex mathematical problems. This comprehensive guide will explore 5 to the fifth power, explaining the concept of exponents, providing multiple ways to calculate the answer, and demonstrating its applications in various fields.
Understanding Exponents
Before diving into 5 to the fifth power, let's establish a firm understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. It's represented as a superscript number to the right of the base. For example, in the expression 5³, 5 is the base, and 3 is the exponent. This means 5 multiplied by itself three times: 5 x 5 x 5 = 125.
Key Terminology:
- Base: The number being multiplied. In 5⁵, 5 is the base.
- Exponent: The number indicating how many times the base is multiplied by itself. In 5⁵, 5 is the exponent.
- Power: The entire expression, base and exponent together. 5⁵ is the power.
Calculating 5 to the Fifth Power
Now, let's address the core question: What is 5 to the fifth power (5⁵)? This means multiplying the base number 5 by itself five times:
5⁵ = 5 x 5 x 5 x 5 x 5
We can calculate this step-by-step:
- 5 x 5 = 25
- 25 x 5 = 125
- 125 x 5 = 625
- 625 x 5 = 3125
Therefore, 5 to the fifth power is 3125.
Alternative Methods for Calculation
While the step-by-step method is straightforward, there are other ways to calculate 5⁵, particularly useful when dealing with larger exponents or different bases.
Using a Calculator
The simplest and often fastest method is to use a calculator. Most calculators have an exponent function (usually represented by a caret symbol "^" or a "xʸ" button). Simply input "5^5" or "5 xʸ 5" and the calculator will instantly provide the answer: 3125.
Using Logarithms (Advanced Method)
For those familiar with logarithms, it's possible to calculate exponents using logarithmic properties. While not the most efficient method for 5⁵, it's a valuable technique for more complex scenarios. The process involves taking the logarithm of the expression, performing calculations, and then using the antilogarithm to obtain the final result.
Utilizing Programming Languages
Programming languages like Python, Java, and C++ offer built-in functions to calculate exponents. These functions typically use more efficient algorithms than manual calculations, making them suitable for handling large exponents or complex calculations. For example, in Python, you could use the ** operator: 5**5 will return 3125.
Applications of Exponentiation
The concept of exponentiation, exemplified by 5⁵, extends far beyond simple mathematical exercises. It has significant applications in various fields:
Science and Engineering
- Compound Interest: Exponentiation is crucial in calculating compound interest, where interest earned is added to the principal, and subsequent interest calculations are based on the increased amount.
- Exponential Growth and Decay: Many natural phenomena, such as population growth, radioactive decay, and the spread of diseases, follow exponential patterns. Understanding exponentiation is key to modeling and predicting these processes.
- Physics and Engineering Calculations: Exponents are frequently used in physics and engineering formulas, particularly in areas like mechanics, electricity, and thermodynamics.
Computer Science
- Big O Notation: In computer science, big O notation uses exponents to describe the complexity of algorithms, indicating how the runtime or memory usage scales with input size.
- Data Structures and Algorithms: Exponentiation is involved in various data structures and algorithms, such as binary trees and exponentiation by squaring.
Finance
- Investment Growth: Calculating the future value of investments often involves exponentiation, particularly when considering compounding effects.
- Loan Amortization: Determining loan payments involves using exponential functions to account for the interest accruing over time.
Statistics and Probability
- Probability Distributions: Several probability distributions, such as the binomial and Poisson distributions, utilize exponential functions in their formulations.
- Statistical Modeling: Exponentiation plays a role in statistical modeling, enabling the creation of models that capture exponential trends and relationships.
Understanding the Significance of 5 to the Fifth Power (3125)
The specific result, 3125, might seem like just a number, but it represents a significant milestone in understanding exponential growth. This number illustrates the rapid increase that occurs when a base number is multiplied by itself repeatedly. Consider this in the context of population growth: if a population increased by a factor of 5 each year, the size would escalate dramatically in just five years, reaching 3125 times its initial size. This dramatic increase highlights the powerful impact of exponential functions in various contexts.
Further Exploration: Beyond 5 to the Fifth Power
This in-depth analysis of 5⁵ provides a solid foundation for exploring more advanced concepts in mathematics. You can expand your understanding by:
- Exploring Negative Exponents: Learn how negative exponents relate to reciprocals.
- Investigating Fractional Exponents: Discover the relationship between fractional exponents and roots.
- Delving into Complex Numbers: Explore how exponentiation applies to complex numbers.
- Studying Exponential Functions and Graphs: Visualize exponential growth and decay using graphs.
By understanding 5 to the fifth power and the broader concept of exponentiation, you gain a powerful tool for tackling diverse mathematical and real-world problems. From understanding compound interest to modeling population growth, the applications are vast and impactful. Remember to utilize the various methods discussed to calculate exponents, choosing the approach that best suits your needs and mathematical background.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 5 To The Fifth Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.