What Is 5 To The Power Of 2
News Co
Mar 15, 2025 · 5 min read
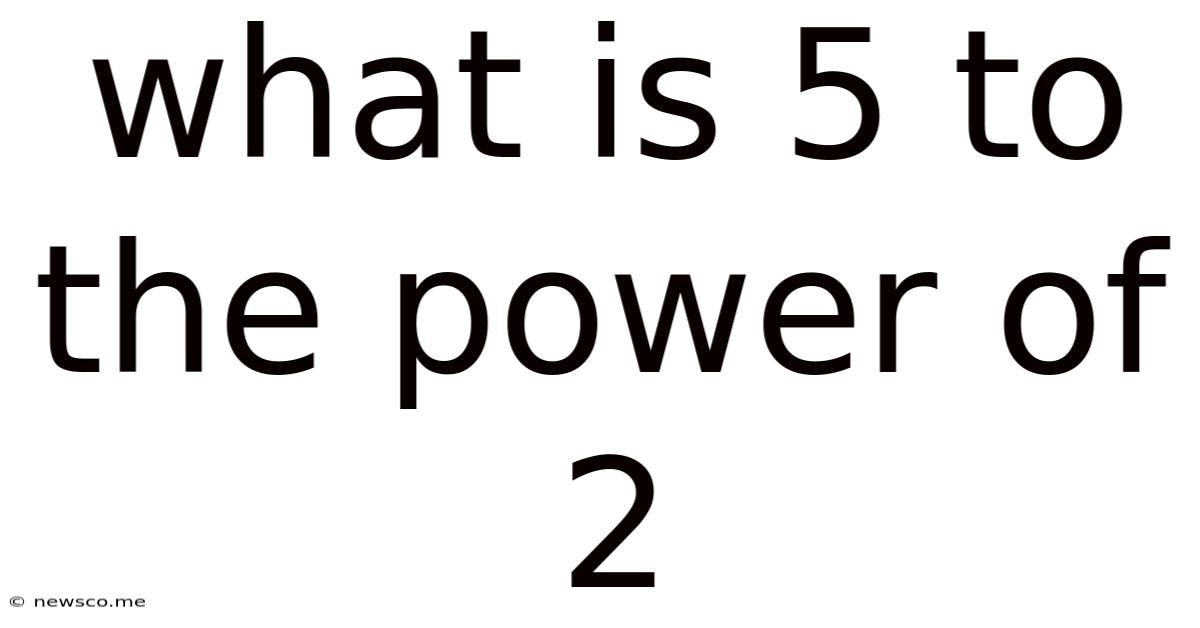
Table of Contents
What is 5 to the Power of 2? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 5 to the power of 2?" opens a door to a vast world of mathematical concepts, with far-reaching applications across various fields. This article will not only answer this specific question but will also delve into the broader concept of exponents, exploring their properties, applications, and significance in mathematics and beyond.
Understanding Exponents: A Foundation in Mathematics
Before tackling 5 to the power of 2, let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. It's represented as a superscript to the right of the base. For example, in the expression 5², the '5' is the base, and the '2' is the exponent. This means 5 is multiplied by itself 2 times: 5 x 5.
Key Terminology:
- Base: The number being multiplied (in 5², the base is 5).
- Exponent: The number indicating how many times the base is multiplied by itself (in 5², the exponent is 2).
- Power: Another term for exponent; 5² is "5 raised to the power of 2".
Calculating 5 to the Power of 2
Now, let's address the central question: What is 5 to the power of 2 (5²)?
5² = 5 x 5 = 25
Therefore, 5 to the power of 2 equals 25. This is a fundamental calculation in arithmetic and serves as a building block for more complex mathematical operations.
Beyond the Basics: Exploring Exponent Properties
Exponents possess several important properties that streamline calculations and are crucial for understanding more advanced mathematical concepts. These properties include:
1. Product of Powers
When multiplying two numbers with the same base, you can add their exponents:
xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾
For example: 5² * 5³ = 5⁽²⁺³⁾ = 5⁵ = 3125
2. Quotient of Powers
When dividing two numbers with the same base, you can subtract their exponents:
xᵃ / xᵇ = x⁽ᵃ⁻ᵇ⁾ (where x ≠ 0)
For example: 5⁵ / 5² = 5⁽⁵⁻²⁾ = 5³ = 125
3. Power of a Power
When raising a power to another power, you multiply the exponents:
(xᵃ)ᵇ = x⁽ᵃ*ᵇ⁾
For example: (5²)³ = 5⁽²*³⁾ = 5⁶ = 15625
4. Power of a Product
When raising a product to a power, you raise each factor to that power:
(xy)ᵃ = xᵃyᵃ
For example: (5 * 2)² = 5² * 2² = 25 * 4 = 100
5. Power of a Quotient
When raising a quotient to a power, you raise both the numerator and the denominator to that power:
(x/y)ᵃ = xᵃ/yᵃ (where y ≠ 0)
For example: (5/2)² = 5²/2² = 25/4 = 6.25
Applications of Exponents: From Simple Calculations to Complex Theories
The concept of exponents extends far beyond simple calculations. Their applications are widespread and crucial across numerous fields:
1. Scientific Notation
Exponents are fundamental in scientific notation, a way of representing very large or very small numbers concisely. For example, the speed of light is approximately 3 x 10⁸ meters per second. The exponent (8) indicates that 3 is multiplied by 10 eight times.
2. Compound Interest
In finance, exponents are used to calculate compound interest. The formula involves raising a base (1 + interest rate) to the power of the number of compounding periods. This helps determine the future value of an investment.
3. Exponential Growth and Decay
Exponents are central to understanding exponential growth and decay phenomena observed in various contexts like population growth, radioactive decay, and the spread of diseases. These processes are modeled using exponential functions, where the variable is in the exponent.
4. Computer Science and Data Structures
Binary numbers, the foundation of computer science, utilize powers of 2. Memory allocation, data structures like trees, and algorithm analysis often leverage exponential concepts.
5. Physics and Engineering
Exponents play a significant role in various physical laws and engineering principles. For instance, Newton's Law of Universal Gravitation incorporates exponents to describe the force of gravity between two objects.
6. Probability and Statistics
Probabilities often involve calculating combinations and permutations, which heavily rely on exponents and factorials (which themselves are built on exponents).
Expanding on the Power of 2: Exploring Higher Powers of 5
While we've focused on 5², exploring higher powers of 5 provides further insight into exponential growth:
- 5³ = 5 x 5 x 5 = 125
- 5⁴ = 5 x 5 x 5 x 5 = 625
- 5⁵ = 5 x 5 x 5 x 5 x 5 = 3125
- 5⁶ = 5 x 5 x 5 x 5 x 5 x 5 = 15625
- and so on...
Notice how rapidly the value increases as the exponent grows. This demonstrates the nature of exponential growth, where the increase becomes increasingly dramatic with each increment of the exponent.
Negative and Fractional Exponents: Extending the Scope
The concept of exponents extends beyond positive integers. Negative exponents represent reciprocals, and fractional exponents involve roots:
1. Negative Exponents
x⁻ⁿ = 1/xⁿ (where x ≠ 0)
For example: 5⁻² = 1/5² = 1/25 = 0.04
2. Fractional Exponents
xᵐ/ⁿ = ⁿ√xᵐ
For example: 5²/³ = ³√5² = ³√25 ≈ 2.924
These extensions significantly broaden the applicability of exponents, enabling the handling of a wider range of mathematical problems.
Conclusion: The Significance of 5 to the Power of 2 and Beyond
The seemingly simple calculation of 5 to the power of 2, resulting in 25, serves as a gateway to a rich and powerful mathematical concept. Understanding exponents, their properties, and their applications is crucial for tackling complex problems across diverse fields. From scientific notation to compound interest, exponential growth to computer science, the concept of exponents underpins numerous aspects of our understanding of the world and the development of technology. Mastering this foundational concept unlocks a deeper appreciation of mathematics and its vital role in shaping our understanding and technological advancements.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.