What Is 5 To The Power Of 6
News Co
Apr 04, 2025 · 4 min read
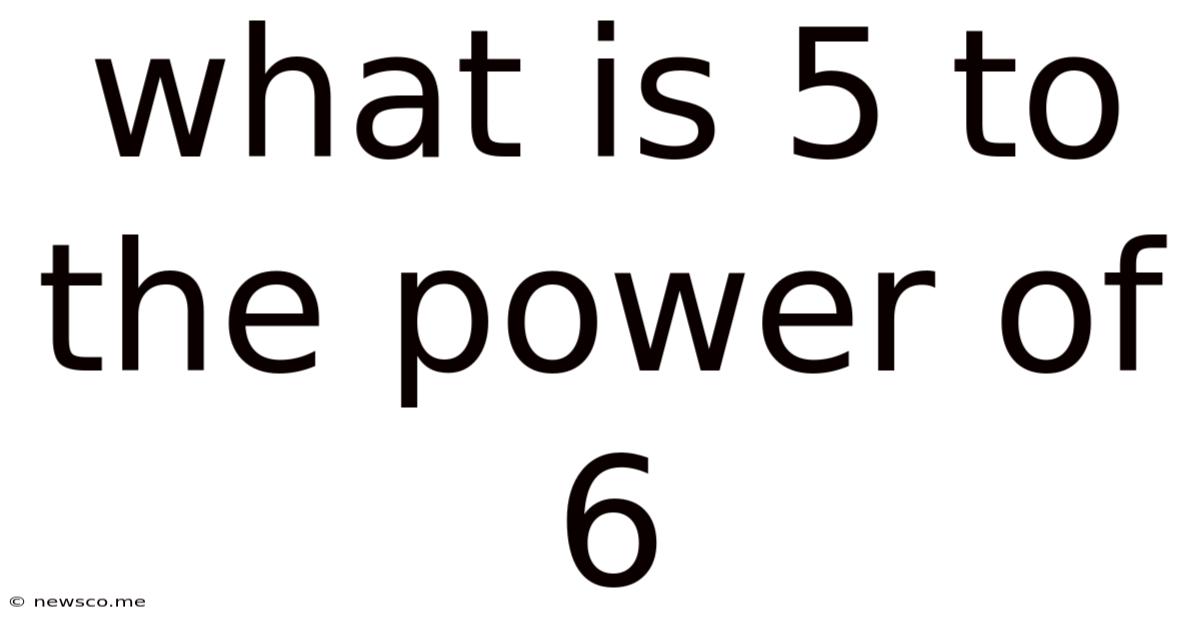
Table of Contents
What is 5 to the Power of 6? A Deep Dive into Exponentiation
The seemingly simple question, "What is 5 to the power of 6?" opens a door to a fascinating world of mathematics, specifically exponentiation. While a calculator readily provides the answer (15625), understanding the underlying concepts and exploring related mathematical ideas significantly enriches the learning experience. This article delves deep into the meaning of 5<sup>6</sup>, its calculation, its applications, and broader implications within mathematics.
Understanding Exponentiation
Exponentiation, at its core, is repeated multiplication. It's a concise way of expressing a number multiplied by itself a certain number of times. The expression a<sup>b</sup> signifies that the base (a) is multiplied by itself b times. In our case, 5<sup>6</sup> means 5 multiplied by itself 6 times: 5 x 5 x 5 x 5 x 5 x 5.
The Components: Base and Exponent
Let's break down the components of 5<sup>6</sup>:
- Base (5): This is the number being multiplied repeatedly.
- Exponent (6): This indicates how many times the base is multiplied by itself. It's also called the power or index.
Understanding these components is crucial to grasping exponentiation and solving more complex problems.
Calculating 5 to the Power of 6
The most straightforward method to calculate 5<sup>6</sup> is through repeated multiplication:
5 x 5 = 25 25 x 5 = 125 125 x 5 = 625 625 x 5 = 3125 3125 x 5 = 15625
Therefore, 5<sup>6</sup> = 15625.
Alternative Calculation Methods
While repeated multiplication is simple for smaller exponents, it becomes cumbersome for larger ones. Let's explore alternative approaches:
-
Using a Calculator: Modern calculators efficiently handle exponentiation. Simply enter 5, press the exponent button (usually denoted as
^orx<sup>y</sup>), enter 6, and press equals. -
Logarithms: For very large exponents, logarithms provide a more efficient method. Logarithms essentially reverse exponentiation. However, for 5<sup>6</sup>, the direct multiplication method is perfectly suitable.
-
Programming Languages: Most programming languages have built-in functions for exponentiation (often represented as
pow(5,6)or a similar notation).
Applications of Exponentiation
Exponentiation isn't just a mathematical curiosity; it has widespread applications across various fields:
1. Compound Interest
In finance, compound interest calculations heavily rely on exponentiation. The formula A = P(1 + r/n)^(nt) uses exponentiation to determine the future value (A) of an investment based on the principal amount (P), interest rate (r), compounding periods (n), and time (t).
2. Scientific Notation
Exponentiation is fundamental to scientific notation, a way of representing very large or very small numbers concisely. For instance, the speed of light (approximately 300,000,000 meters per second) can be written as 3 x 10<sup>8</sup> m/s.
3. Computer Science
Exponentiation plays a vital role in computer algorithms and data structures. For example, the time complexity of certain algorithms (like binary search) is expressed using exponential notation. Furthermore, many cryptographic systems rely on exponentiation with very large numbers.
4. Physics and Engineering
Many physical phenomena are modeled using exponential functions. Examples include radioactive decay, population growth, and the behavior of certain electrical circuits.
5. Probability and Statistics
Exponentiation appears in various probability distributions, like the binomial distribution and the Poisson distribution, which are used to model and analyze random events.
Expanding on the Concept: Exploring Related Mathematical Ideas
Understanding 5<sup>6</sup> opens avenues to explore related mathematical concepts:
1. Powers of 5
Let's examine the pattern of powers of 5:
5<sup>1</sup> = 5 5<sup>2</sup> = 25 5<sup>3</sup> = 125 5<sup>4</sup> = 625 5<sup>5</sup> = 3125 5<sup>6</sup> = 15625
Notice the pattern in the last digits: 5, 5, 5, 5, 5, 5. This is because any positive integer power of 5 always ends in 5. This observation showcases the elegance and predictability within mathematical patterns.
2. Negative Exponents
What about 5<sup>-6</sup>? Negative exponents represent reciprocals. 5<sup>-6</sup> is equivalent to 1/5<sup>6</sup> = 1/15625. This introduces the concept of inverse operations in exponentiation.
3. Fractional Exponents
Fractional exponents represent roots. For instance, 5<sup>1/2</sup> is the square root of 5, and 5<sup>1/3</sup> is the cube root of 5. These concepts extend the application of exponentiation to include root calculations.
4. Exponential Growth and Decay
Exponential functions, which utilize exponentiation, model phenomena exhibiting exponential growth or decay. Understanding 5<sup>6</sup> lays the foundation for understanding these broader mathematical concepts used to model real-world situations like population growth or radioactive decay.
Conclusion: Beyond the Calculation
While the answer to "What is 5 to the power of 6?" is 15625, the true value lies in the understanding gained through exploring the underlying concepts and related mathematical ideas. Exponentiation is a fundamental operation with far-reaching applications across numerous disciplines. By delving deeper into its properties and implications, we gain a richer appreciation of the elegance and power of mathematics and its ability to model and explain the world around us. This simple calculation serves as a springboard for a much broader and more fascinating mathematical journey.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 5 To The Power Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.