What Is 50 Percent Of 80
News Co
Apr 16, 2025 · 5 min read
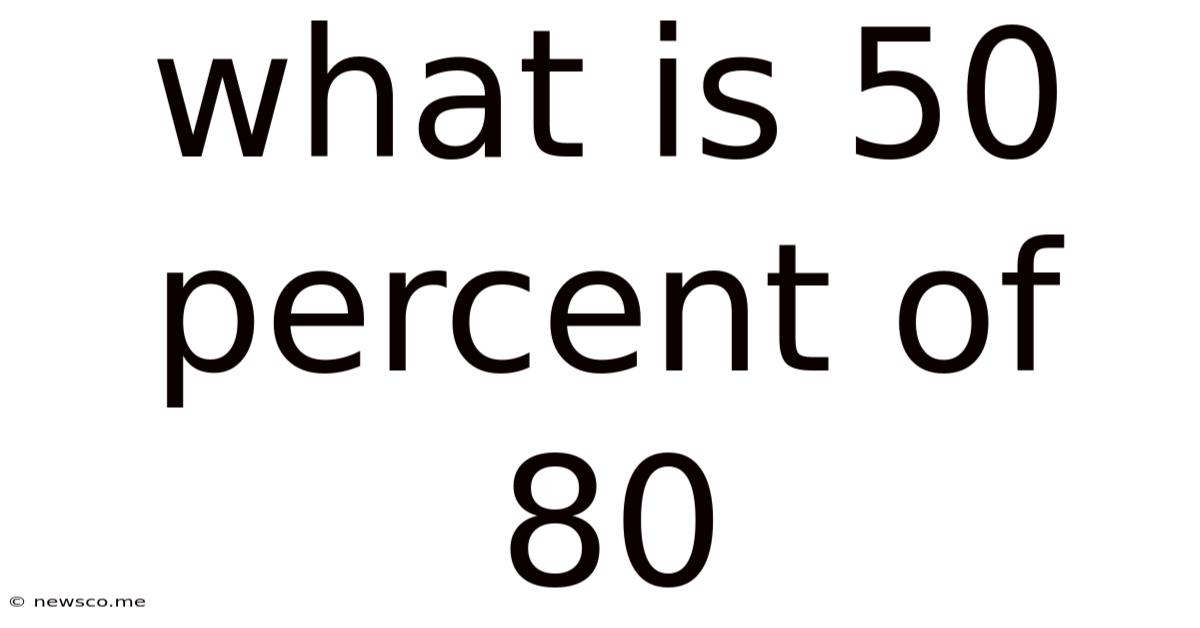
Table of Contents
What is 50 Percent of 80? A Deep Dive into Percentages and Their Applications
Finding 50 percent of 80 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics and its widespread applications across various fields. This article will not only answer the question directly but also explore the broader context of percentages, providing you with a comprehensive understanding of this crucial mathematical tool.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 50 percent means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
This fundamental understanding is key to solving almost any percentage problem. We can use this knowledge to easily determine what 50% of 80 is.
Calculating 50% of 80
The most straightforward method is to convert the percentage to a decimal and then multiply it by the number. Since 50% is equal to 0.5, we simply multiply 0.5 by 80:
0.5 * 80 = 40
Therefore, 50% of 80 is 40.
Alternative Methods for Calculating Percentages
While the decimal method is efficient, there are other ways to calculate percentages, especially useful for mental calculations or when dealing with less straightforward percentages.
Method 1: Using Fractions
As mentioned earlier, 50% is equivalent to the fraction 1/2. To find 50% of 80, we can multiply 80 by 1/2:
(1/2) * 80 = 80/2 = 40
This method is particularly helpful when dealing with percentages like 25% (1/4), 75% (3/4), and others that have simple fractional equivalents.
Method 2: Finding 10% and Scaling Up
This method is excellent for mental calculations. First, find 10% of 80 by dividing it by 10:
80 / 10 = 8
Since 50% is five times 10%, we multiply the result by 5:
8 * 5 = 40
This approach is particularly useful for percentages that are multiples of 10 (like 20%, 30%, etc.).
Method 3: Using Proportions
This method utilizes the concept of ratios and proportions. We can set up a proportion to solve for the unknown value (x), which represents 50% of 80:
50/100 = x/80
Cross-multiplying gives us:
50 * 80 = 100 * x
4000 = 100x
Dividing both sides by 100 gives:
x = 40
This method is more versatile and can be applied to any percentage calculation.
Real-World Applications of Percentage Calculations
Understanding percentages is crucial in numerous everyday situations:
1. Finance and Budgeting:
- Discounts: Calculating discounts on sale items. For example, a 20% discount on a $100 item.
- Interest Rates: Determining interest earned on savings accounts or interest paid on loans.
- Taxes: Calculating sales tax, income tax, or property tax.
- Investment Returns: Tracking the performance of investments and calculating returns.
2. Science and Data Analysis:
- Statistical Analysis: Representing data in terms of percentages to visualize trends and relationships.
- Experimental Results: Expressing experimental results as percentages to indicate success rates or error margins.
- Scientific Research: Analyzing data and presenting findings using percentages.
3. Everyday Life:
- Tip Calculation: Determining the appropriate tip amount in restaurants.
- Grade Calculation: Calculating your overall grade in a course based on individual assignment scores.
- Cooking: Scaling up or down recipes based on percentage adjustments.
- Shopping: Comparing prices and finding the best deals based on discounts and unit prices.
Beyond 50% of 80: Mastering Percentage Calculations
While we've focused on calculating 50% of 80, the principles discussed apply to any percentage calculation. The key is to understand the fundamental concept of percentages as fractions of 100 and to choose the most efficient method for the calculation at hand.
Whether you use the decimal method, the fractional method, the 10% scaling method, or the proportion method, consistency and practice will help you become proficient in percentage calculations. With practice, you'll find that these calculations become second nature, allowing you to navigate various financial, scientific, and everyday situations with confidence.
Advanced Percentage Calculations: Handling More Complex Scenarios
The methods outlined above provide a solid foundation for basic percentage calculations. However, real-world problems often involve more complex scenarios. Let's explore some of these:
1. Calculating Percentage Increase or Decrease:
This involves finding the percentage change between two numbers. The formula is:
Percentage Change = [(New Value - Old Value) / Old Value] * 100%
For example, if a product's price increased from $50 to $60, the percentage increase is:
[(60 - 50) / 50] * 100% = 20%
2. Finding the Original Value after a Percentage Change:
If you know the final value and the percentage change, you can calculate the original value. This often involves working backward using the percentage change formula.
For instance, if a price increased by 15% to $115, the original price (x) can be found using the equation:
x + 0.15x = 115
1.15x = 115
x = 100
The original price was $100.
3. Compound Percentage Changes:
When dealing with multiple percentage changes applied successively, the order matters. You cannot simply add the percentages. Instead, you must apply each percentage change sequentially to the result of the previous change.
For example, a 10% increase followed by a 10% decrease does not result in no change.
Utilizing Technology for Percentage Calculations
In today's digital world, various tools can assist with percentage calculations:
- Spreadsheets (Excel, Google Sheets): These offer built-in functions for percentage calculations, making complex computations easier.
- Calculators: Most calculators have a percentage function that simplifies calculations significantly.
- Online Percentage Calculators: Numerous websites provide online calculators specifically designed for percentage calculations, offering a convenient solution for quick calculations.
Conclusion: The Enduring Importance of Percentages
Understanding percentages is not merely an academic exercise; it's a vital life skill. From managing personal finances to analyzing data in professional settings, the ability to calculate and interpret percentages is essential for informed decision-making. While the calculation of 50% of 80 serves as a simple starting point, mastering percentage calculations opens up a world of possibilities, empowering you to navigate the quantitative aspects of life with confidence and efficiency. Remember to practice regularly, exploring different methods and applying your knowledge to real-world problems to reinforce your understanding and build your skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 50 Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.