What Is 6.25 In Fraction Form
News Co
Apr 06, 2025 · 5 min read
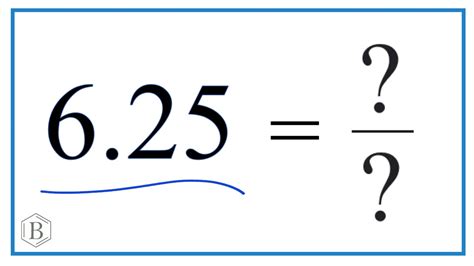
Table of Contents
What is 6.25 in Fraction Form? A Comprehensive Guide
Converting decimals to fractions might seem daunting at first, but it's a fundamental skill with widespread applications in mathematics, science, and everyday life. This comprehensive guide will walk you through the process of converting the decimal 6.25 into its fractional equivalent, explaining the method step-by-step and exploring related concepts to solidify your understanding. We'll also delve into the practical uses of understanding decimal-fraction conversions.
Understanding Decimals and Fractions
Before we dive into the conversion, let's refresh our understanding of decimals and fractions.
Decimals: Decimals represent numbers less than one using a base-ten system. The position of a digit to the right of the decimal point indicates its place value (tenths, hundredths, thousandths, etc.). For example, in the decimal 6.25, the '6' represents 6 whole units, the '2' represents 2 tenths (2/10), and the '5' represents 5 hundredths (5/100).
Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many parts the whole is divided into. For example, the fraction 1/2 represents one part of a whole that's divided into two equal parts.
Converting 6.25 to a Fraction: A Step-by-Step Approach
The conversion of 6.25 to a fraction involves several straightforward steps:
Step 1: Identify the Place Value of the Last Digit
The last digit in 6.25 is '5', which is in the hundredths place. This tells us that the denominator of our fraction will be 100.
Step 2: Write the Decimal as a Fraction
We can write 6.25 as a fraction by placing the digits after the decimal point (25) over the denominator (100):
6.25 = 6 and 25/100
Step 3: Simplify the Fraction (if possible)
The fraction 25/100 can be simplified by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 25 and 100 is 25. We divide both the numerator and the denominator by the GCD:
25 ÷ 25 = 1 100 ÷ 25 = 4
Therefore, 25/100 simplifies to 1/4.
Step 4: Combine the Whole Number and the Simplified Fraction
We now have 6 and 1/4. To express this as an improper fraction (where the numerator is larger than the denominator), we multiply the whole number by the denominator and add the numerator:
(6 x 4) + 1 = 25
The new numerator is 25, and the denominator remains 4. Therefore, 6.25 as an improper fraction is 25/4.
Therefore, 6.25 in fraction form is 25/4 or 6 and 1/4.
Different Methods for Decimal to Fraction Conversion
While the above method is the most straightforward for 6.25, let's explore some alternative approaches applicable to other decimals:
Method 1: Using Place Value Directly (for terminating decimals)
This method is efficient for decimals that terminate (end). You identify the place value of the last digit, use that as the denominator, and place the digits after the decimal point as the numerator. Then simplify the fraction.
Method 2: Using a Power of 10 (for terminating decimals)
Similar to Method 1, but instead of directly identifying the place value, you multiply the decimal by a power of 10 (10, 100, 1000, etc.) to make it a whole number. This power of 10 becomes the denominator of the fraction.
Method 3: Repeating Decimals (requires a different approach)
Repeating decimals (like 0.333...) require a slightly different approach involving algebraic manipulation to convert them to fractions. This is beyond the scope of this specific example but is a valuable topic to explore separately.
Practical Applications of Decimal-Fraction Conversions
Understanding decimal-fraction conversions is crucial in various contexts:
1. Cooking and Baking: Recipes often use both fractions (e.g., 1/2 cup) and decimals (e.g., 0.75 cups). Converting between the two is essential for accurate measurements.
2. Engineering and Construction: Precise measurements are paramount in these fields. Converting between decimals and fractions ensures accuracy in blueprints and calculations.
3. Finance: Interest rates, stock prices, and other financial figures are frequently expressed as decimals. Converting them to fractions can help in understanding the proportions and relationships involved.
4. Science: Many scientific measurements and calculations involve both decimals and fractions. The ability to convert between them is necessary for accurate analysis and interpretation of data.
5. Everyday Calculations: From splitting bills to calculating discounts, understanding decimal-fraction conversions makes everyday calculations easier and more precise.
Troubleshooting Common Errors
While converting decimals to fractions is generally straightforward, some common errors can occur:
-
Incorrect Place Value Identification: Double-check the place value of the last digit to ensure the correct denominator is used.
-
Failure to Simplify: Always simplify the fraction to its lowest terms for a concise and accurate representation.
-
Improper Handling of Whole Numbers: Remember to correctly incorporate the whole number part of the decimal when converting to a mixed or improper fraction.
Expanding Your Knowledge
This guide provides a foundational understanding of converting decimals like 6.25 to fractions. To further enhance your skills, explore additional resources on:
-
Converting repeating decimals to fractions: This requires a more advanced approach using algebraic manipulation.
-
Converting fractions to decimals: This is the inverse process and equally important to master.
-
Working with mixed numbers: Understanding how to convert between mixed numbers (e.g., 6 and 1/4) and improper fractions is crucial.
-
Performing arithmetic operations with fractions and decimals: Practice adding, subtracting, multiplying, and dividing fractions and decimals.
By mastering these concepts, you'll significantly improve your mathematical abilities and gain a deeper understanding of how numbers are represented and manipulated. The ability to seamlessly convert between decimals and fractions is a valuable skill applicable to many aspects of life, from everyday calculations to specialized fields. Remember to practice regularly to solidify your understanding and build confidence in your abilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 6.25 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.