What Is 6 To The Power Of 3
News Co
Mar 18, 2025 · 5 min read
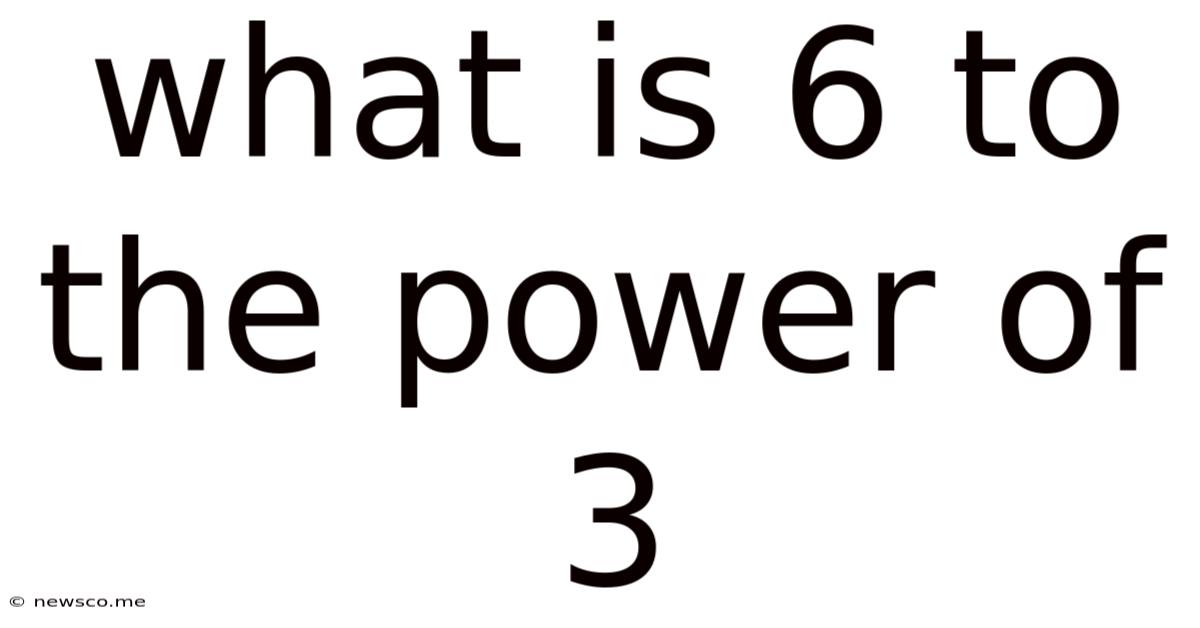
Table of Contents
What is 6 to the Power of 3? A Deep Dive into Exponentiation
The seemingly simple question, "What is 6 to the power of 3?" opens a door to a fascinating world of mathematics, specifically exponentiation. While the answer itself is straightforward – 216 – understanding the underlying concepts provides a robust foundation for more complex mathematical explorations. This article will delve into not just the answer, but the meaning, applications, and broader implications of 6<sup>3</sup> and exponentiation in general.
Understanding Exponentiation: Beyond Simple Multiplication
Exponentiation, at its core, represents repeated multiplication. It's a shorthand way of expressing a number multiplied by itself a certain number of times. The expression 6<sup>3</sup>, read as "6 to the power of 3" or "6 cubed," signifies 6 multiplied by itself three times: 6 x 6 x 6.
The Components of an Exponent
Every exponential expression has two key components:
- Base: The number being multiplied (in this case, 6).
- Exponent: The number indicating how many times the base is multiplied by itself (in this case, 3).
Understanding these components is crucial for solving any exponential problem. The exponent sits slightly elevated, indicating its distinct role in the operation.
Calculating 6 to the Power of 3
The calculation itself is straightforward:
6 x 6 = 36 36 x 6 = 216
Therefore, 6 to the power of 3 equals 216.
Alternative Calculation Methods
While the stepwise multiplication above is clear and intuitive, other methods exist, especially helpful for larger exponents:
-
Using a calculator: Most calculators have an exponent function (often denoted as x<sup>y</sup> or ^). Simply enter 6, press the exponent function, enter 3, and press equals.
-
Logarithms (for more advanced calculations): Logarithms are the inverse of exponentiation. While not necessary for 6<sup>3</sup>, they become essential for solving equations where the exponent is unknown.
Applications of Exponentiation: Real-World Examples
Exponentiation isn't confined to abstract mathematical exercises; it finds widespread application in diverse fields:
1. Geometry and Volume Calculations
Consider a cube with sides of length 6 units. The volume of the cube is calculated by cubing the side length: 6<sup>3</sup> = 216 cubic units. This principle extends to calculating the volume of other three-dimensional shapes.
2. Compound Interest and Financial Growth
Compound interest, where interest earned is added to the principal, leading to exponential growth, is a prime example. If you invest $1000 at an interest rate of 6% compounded annually, the calculation involves exponentiation to determine the future value after several years.
3. Scientific Notation and Large Numbers
Exponentiation is crucial in representing extremely large or small numbers using scientific notation. For instance, the speed of light is approximately 3 x 10<sup>8</sup> meters per second. The exponent, 8, represents the magnitude of the number.
4. Computer Science and Data Storage
In computer science, exponentiation is used in algorithms, particularly those related to data structures and complexity analysis. The growth rate of algorithms often follows exponential patterns. Data storage capacity is also often expressed in powers of 2 (e.g., kilobytes, megabytes, gigabytes).
5. Population Growth Models
Exponential growth is frequently observed in biological populations. Under ideal conditions, a population can grow exponentially, meaning its size increases by a certain factor over time. This growth can be modeled using exponential functions.
Expanding on Exponents: Beyond Integer Exponents
While 6<sup>3</sup> uses an integer exponent, exponentiation extends beyond this:
1. Fractional Exponents: Roots and Radicals
Fractional exponents represent roots. For example, 6<sup>1/2</sup> is the square root of 6, and 6<sup>1/3</sup> is the cube root of 6.
2. Negative Exponents: Reciprocals
A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example, 6<sup>-2</sup> = 1/6<sup>2</sup> = 1/36.
3. Zero Exponent: The Identity
Any non-zero number raised to the power of 0 equals 1. Therefore, 6<sup>0</sup> = 1. This is a fundamental property of exponents.
4. Decimal Exponents: Interpolation and Approximation
Decimal exponents can be calculated using logarithms or approximations, yielding values between whole-number powers.
The Significance of 6 Cubed in Specific Contexts
While 216 itself might not have a singularly profound meaning in every context, its appearance as 6<sup>3</sup> connects it to specific mathematical and geometrical relationships:
-
Perfect Number Properties: While 216 is not a perfect number (a number equal to the sum of its proper divisors), its factors and divisors are connected to the broader study of number theory.
-
Cubic Geometry: As previously mentioned, 216 represents the volume of a cube with 6-unit sides. This connects the number to concepts of spatial dimensions and volume calculations.
Beyond Calculation: The Conceptual Importance of Exponentiation
Understanding 6<sup>3</sup> goes beyond simple calculation. It's a gateway to appreciating the power and elegance of mathematical notation and its applications in various fields. The concept of exponentiation underpins many mathematical models used to describe the real world, including growth, decay, and complexity.
Conclusion: Mastering Exponents for a Broader Understanding
The question "What is 6 to the power of 3?" seemingly has a simple answer: 216. However, this exploration has unveiled the rich tapestry of concepts connected to exponentiation. From simple calculations to complex mathematical models, understanding exponents is crucial for navigating numerous academic and real-world applications. By grasping the fundamental principles and extending knowledge to fractional, negative, and decimal exponents, one gains a more profound understanding of mathematics and its capacity to model and explain the world around us. This knowledge forms a solid foundation for future mathematical endeavors and enhances problem-solving abilities across various disciplines. The seemingly simple calculation of 6<sup>3</sup> becomes a stepping stone to a deeper appreciation of the power and versatility of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 6 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.