What Is 60 Off Of 25
News Co
Apr 04, 2025 · 4 min read
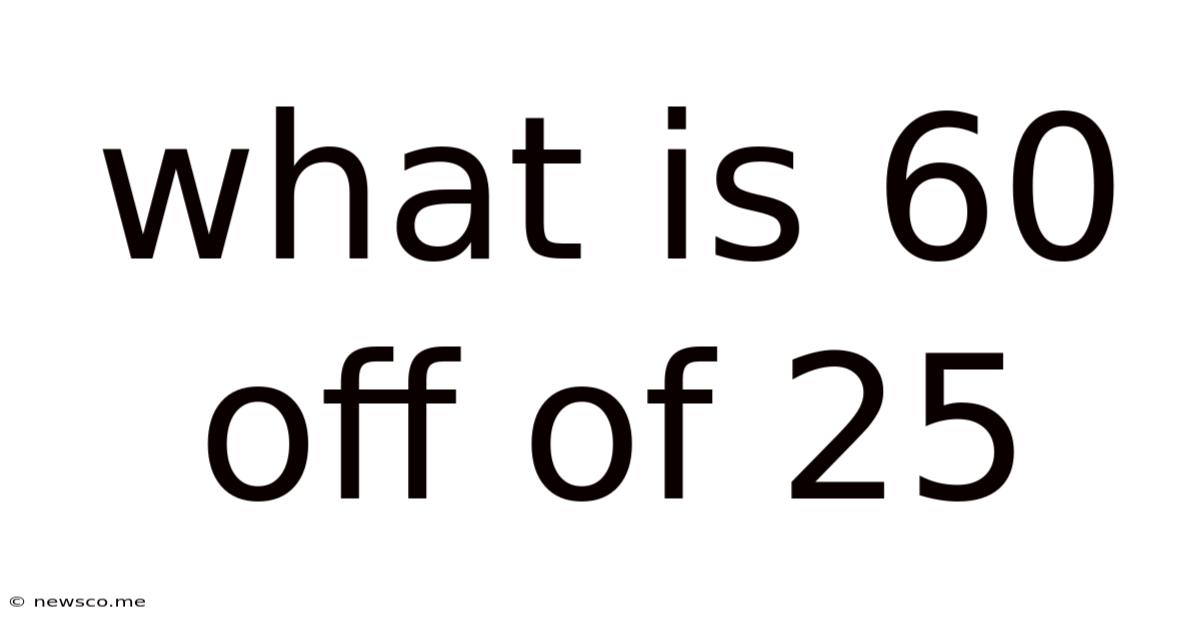
Table of Contents
What is 60% Off of 25? A Comprehensive Guide to Percentage Calculations
Calculating discounts is a crucial skill in everyday life, from shopping for groceries to understanding sales promotions. This comprehensive guide will not only answer the question "What is 60% off of 25?" but also equip you with the knowledge and methods to tackle similar percentage calculations with confidence. We'll cover various approaches, from simple arithmetic to using formulas and helpful tools.
Understanding Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred." So, 60% means 60 out of 100, or 60/100, which simplifies to 3/5.
Method 1: The Fraction Method
This method is intuitive and easy to understand, especially for smaller numbers. We break down the problem into its fractional components.
Steps:
-
Convert the percentage to a fraction: 60% is equivalent to 60/100, which simplifies to 3/5.
-
Multiply the fraction by the original amount: Multiply 3/5 by 25: (3/5) * 25 = 15
-
Interpret the result: The result, 15, represents the amount of the discount. This means a 60% discount on 25 is 15.
-
Calculate the final price: Subtract the discount from the original price: 25 - 15 = 10. Therefore, the final price after a 60% discount is 10.
Method 2: The Decimal Method
This method utilizes decimal equivalents of percentages, making it suitable for calculations involving larger numbers or more complex scenarios.
Steps:
-
Convert the percentage to a decimal: Divide the percentage by 100. 60% / 100 = 0.6
-
Multiply the decimal by the original amount: Multiply 0.6 by 25: 0.6 * 25 = 15
-
Interpret the result: Similar to the fraction method, the result, 15, is the discount amount.
-
Calculate the final price: Subtract the discount from the original price: 25 - 15 = 10. The final price is 10.
Method 3: Using a Proportion
This method is a classic approach to solving percentage problems and offers a clear visual representation of the relationship between the parts and the whole.
Steps:
-
Set up a proportion: We can set up a proportion as follows:
x / 25 = 60 / 100where 'x' represents the discount amount.
-
Cross-multiply: Cross-multiplying gives us:
100x = 60 * 25100x = 1500 -
Solve for x: Divide both sides by 100:
x = 1500 / 100x = 15 -
Interpret and calculate the final price: The discount is 15, and the final price is 25 - 15 = 10.
Method 4: Using a Calculator
Most calculators have a percentage function that simplifies these calculations. Simply enter 25, press the multiplication key, then enter 60 and the percentage key (%). The calculator will directly give you the discount amount (15). Subtract this from the original price (25) to get the final price (10).
Expanding on Percentage Calculations: Real-World Applications
Understanding percentage calculations extends far beyond simple discounts. Let's explore some real-world applications:
1. Sales Tax
Sales tax is calculated as a percentage of the purchase price. For example, if the sales tax in your area is 8%, and you buy an item for $50, the sales tax would be 8% of $50, or $4.
2. Tips and Gratuities
Restaurants often suggest a certain percentage for tips, usually 15%, 18%, or 20%. If your bill is $75 and you want to leave a 20% tip, you calculate 20% of $75, which is $15.
3. Interest Rates
Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding these percentages is crucial for making informed financial decisions.
4. Profit Margins
Businesses use percentages to calculate their profit margins, representing the percentage of revenue remaining after deducting costs.
5. Analyzing Statistics
Percentages are fundamental in interpreting statistical data, allowing for comparisons and drawing conclusions from data sets.
Common Mistakes to Avoid
While percentage calculations are relatively straightforward, certain mistakes can occur:
- Confusing percentage change with percentage of: Don't confuse a 60% increase from 25 with a 60% discount from 25. These are distinct calculations.
- Incorrect decimal placement: When converting percentages to decimals, ensure the decimal point is placed correctly.
- Misinterpreting the final price: Always remember to subtract the discount amount from the original price to get the final price.
Advanced Percentage Calculations
Let's delve into slightly more complex percentage problems:
Scenario 1: Finding the original price after a discount:
Suppose an item is sold for $20 after a 20% discount. To find the original price, we can use the following formula:
Original Price = Discounted Price / (1 - Discount Rate)
Original Price = $20 / (1 - 0.20) = $20 / 0.80 = $25
Scenario 2: Calculating percentage increase or decrease:
To calculate the percentage increase or decrease between two numbers, use the following formula:
Percentage Change = [(New Value - Old Value) / Old Value] * 100
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill for navigating various aspects of daily life. By understanding the different methods presented in this guide and practicing regularly, you can confidently tackle a wide range of percentage problems. Remember the key is to understand the underlying principles and choose the method that best suits your situation. Practice makes perfect, so continue working through examples and applying these techniques in your daily calculations. With consistent practice, you'll become proficient in calculating percentages effortlessly.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 60 Off Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.