What Is 60 Percent Of 15
News Co
Apr 22, 2025 · 5 min read
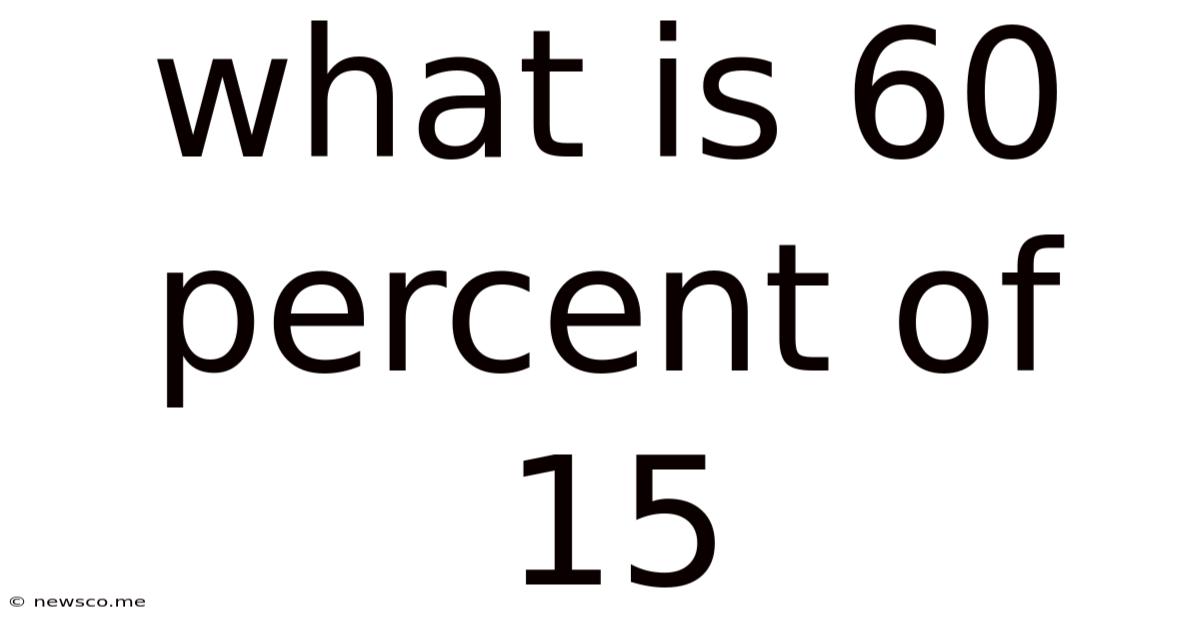
Table of Contents
What is 60 Percent of 15? A Deep Dive into Percentage Calculations
The seemingly simple question, "What is 60 percent of 15?" opens the door to a broader understanding of percentages, their applications, and how to solve them efficiently. While the answer itself is quickly calculable, exploring the different methods and the underlying mathematical principles provides valuable insight applicable to a wide range of situations. This article will delve into multiple ways to solve this problem, explain the concepts involved, and showcase the practical applications of percentage calculations.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). This representation allows for easy comparison and understanding of proportions. For example, 60% means 60 out of 100, or 60/100, which simplifies to 3/5.
This fundamental understanding is crucial for tackling percentage problems. Knowing that a percentage represents a portion of a whole is key to setting up the correct equation.
Method 1: The Classic Formula
The most common method for calculating percentages involves using a simple formula:
Percentage × Whole Number = Part
In our case:
- Percentage: 60% (or 0.60 as a decimal)
- Whole Number: 15
Therefore, the calculation becomes:
0.60 × 15 = 9
Therefore, 60% of 15 is 9.
Method 2: Fraction Conversion
Percentages can be easily converted into fractions. As mentioned earlier, 60% is equivalent to 60/100, which simplifies to 3/5. Using this fraction, we can solve the problem:
(3/5) × 15 = 9
This method provides an alternative approach and reinforces the connection between fractions and percentages.
Method 3: Proportion Method
This method utilizes the concept of ratios and proportions. We set up a proportion:
60/100 = x/15
Where 'x' represents the unknown value (60% of 15). To solve for 'x', we cross-multiply:
60 × 15 = 100 × x
900 = 100x
x = 900/100
x = 9
This method demonstrates the proportional relationship between the percentage and the part of the whole.
Method 4: Using a Calculator
For quick calculations, a simple calculator is the most convenient tool. Simply input "0.60 * 15" to obtain the answer: 9. While this is the fastest method, understanding the underlying principles remains crucial for more complex scenarios and problem-solving.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life, across numerous fields. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding 60% of a loan amount or a 60% discount on an item requires these skills.
-
Retail: Sales, discounts, and markups are expressed as percentages. Determining the final price after a discount or the profit margin on a product requires calculating percentages.
-
Science: Data analysis and scientific research often involve representing data as percentages, for example, the percentage of a population exhibiting a certain characteristic or the percentage change in a measured variable.
-
Statistics: Statistical analysis uses percentages extensively in presenting data, such as the percentage of respondents agreeing with a certain opinion or the percentage change in a statistical measure over time.
-
Everyday Life: Calculating tips in restaurants, determining the percentage of a task completed, or understanding statistics presented in news reports all require understanding percentages.
Expanding the Understanding: Beyond 60% of 15
While this article focused on "What is 60 percent of 15?", the principles discussed are readily applicable to a vast range of percentage problems. Let's consider a few variations:
-
Finding the percentage: If you know the part and the whole, you can calculate the percentage. For example, if 9 is 60% of a number, what is that number? You'd set up the equation: 0.60x = 9, solving for x (which would be 15).
-
Finding the whole: If you know the part and the percentage, you can find the whole. For example, if 6 is 20% of a number, what is that number? Solving 0.20x = 6 gives x = 30.
-
Complex scenarios: Many real-world scenarios involve multiple percentage calculations. For instance, calculating the final price of an item after applying multiple discounts or taxes requires a step-by-step approach using the principles described above.
Mastering Percentages: Tips and Tricks
-
Decimal Conversion: Converting percentages to decimals simplifies calculations. Remember that 60% is equivalent to 0.60.
-
Fraction Simplification: Simplifying fractions before performing calculations often makes the process easier.
-
Practice Regularly: The best way to master percentage calculations is through consistent practice. Work through various examples, including those with more complex scenarios.
-
Understand the Concepts: Focusing on understanding the underlying principles, rather than simply memorizing formulas, will enhance your ability to solve a wider range of percentage problems.
Conclusion: More Than Just a Calculation
"What is 60 percent of 15?" is more than a simple arithmetic question. It's a gateway to understanding the fundamental concepts of percentages, their diverse applications, and their importance in various aspects of life. By mastering the methods and principles outlined in this article, you'll be well-equipped to handle percentage calculations confidently and effectively, unlocking a deeper understanding of quantitative information in numerous contexts. This knowledge isn't limited to mathematical problems; it translates directly to practical decision-making across personal and professional spheres. Practice consistently, and you’ll soon find that percentages are no longer intimidating but rather, a powerful tool for making sense of the world around you.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 60 Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.