What Is 60 Percent Of 20
News Co
Mar 29, 2025 · 5 min read
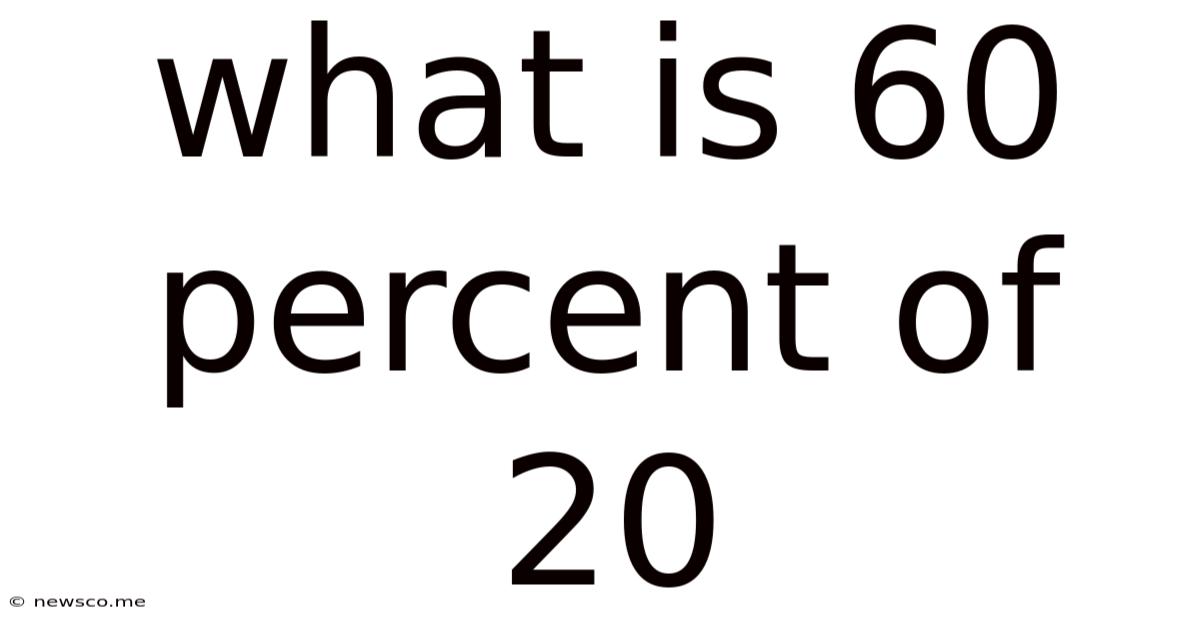
Table of Contents
What is 60 Percent of 20? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. This article will not only answer the question, "What is 60 percent of 20?" but also provide a comprehensive understanding of percentages, their calculation methods, and practical examples showcasing their real-world relevance.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ("per cent" from Latin). Therefore, 60% means 60 out of 100, or 60/100. This can be simplified to 3/5.
Understanding this foundational concept is crucial before tackling any percentage calculation. Percentages are used to represent proportions, rates, and changes in various quantities. They provide a standardized way to compare different values relative to a whole.
Calculating 60 Percent of 20: Methods and Solutions
There are several methods to determine 60 percent of 20. Let's explore the most common approaches:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent by dividing by 100:
60% = 60/100 = 0.6
Then, we multiply this decimal by the number we're finding the percentage of:
0.6 * 20 = 12
Therefore, 60 percent of 20 is 12.
Method 2: Using Fractions
As mentioned earlier, 60% can be expressed as the fraction 60/100 or its simplified form, 3/5. We can then solve the problem using this fraction:
(3/5) * 20 = (3 * 20) / 5 = 60 / 5 = 12
Again, we arrive at the answer: 60 percent of 20 is 12.
Method 3: Using Proportion
This method involves setting up a proportion:
60/100 = x/20
Where 'x' represents the unknown value (60% of 20). To solve for x, we cross-multiply:
100x = 60 * 20
100x = 1200
x = 1200 / 100
x = 12
This confirms our previous results: 60 percent of 20 is 12.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-life scenarios. Here are some examples:
1. Finance and Budgeting:
- Calculating discounts: Imagine a $20 item is on sale with a 60% discount. Knowing that 60% of $20 is $12, you can quickly determine the final price ($20 - $12 = $8).
- Understanding interest rates: Interest on loans or savings accounts is often expressed as a percentage. Calculating percentage increases or decreases helps in financial planning and investment decisions.
- Analyzing tax rates: Tax rates are typically represented as percentages. Understanding how to calculate these helps in budgeting and financial forecasting.
- Profit margins: Businesses use percentage calculations to determine their profit margins (profit as a percentage of revenue).
2. Shopping and Sales:
- Discount calculations: As mentioned above, calculating discounts is crucial for savvy shopping. Understanding percentage discounts allows consumers to make informed purchase decisions.
- Sales tax: Calculating sales tax, which is a percentage of the purchase price, is essential to determine the total cost of an item.
- Comparing prices: Percentages can help in comparing prices of similar products from different stores, considering discounts and sales tax.
3. Science and Statistics:
- Data analysis: Percentages are fundamental in statistical analysis, often used to represent proportions, frequencies, and changes in data sets.
- Experimental results: Scientific experiments often involve percentage calculations to analyze and interpret results. For example, the percentage of successful trials in an experiment.
- Population demographics: Percentages are extensively used to represent population demographics, such as the percentage of the population within specific age groups or with particular characteristics.
4. Everyday Life:
- Tip calculations: Calculating a tip at a restaurant, often expressed as a percentage of the bill, is a common application of percentage calculations.
- Grade calculations: Students often need to calculate their grade percentages based on individual assignment scores and overall class performance.
- Recipe scaling: Adjusting ingredient quantities in recipes based on a percentage increase or decrease is a common culinary application.
Advanced Percentage Calculations: Beyond the Basics
While calculating 60% of 20 is a relatively simple calculation, more complex scenarios require a deeper understanding of percentage manipulation. Here are a few examples:
1. Finding the Percentage Increase or Decrease:
Imagine a value increases from 20 to 26. To find the percentage increase, we first calculate the difference (26 - 20 = 6), then divide by the original value (6/20 = 0.3) and multiply by 100 to express it as a percentage (0.3 * 100 = 30%). Therefore, there is a 30% increase. Percentage decreases are calculated similarly.
2. Finding the Original Value:
If you know that 60% of a number is 12, and you want to find the original number, you can set up an equation:
0.6x = 12
x = 12 / 0.6
x = 20
This demonstrates the reverse calculation – finding the original value given a percentage and its resulting value.
3. Compound Percentages:
Compound percentages involve applying a percentage change to a value, then applying another percentage change to the resulting value. This is frequently used in financial calculations, such as compound interest.
Conclusion: The Ubiquity of Percentages
The ability to calculate percentages accurately and efficiently is a critical skill applicable across numerous fields. From basic everyday tasks to complex financial and scientific applications, the concepts discussed in this article equip individuals with the fundamental understanding and methods for navigating the world of percentages effectively. Mastering percentage calculations unlocks a deeper understanding of quantitative information and empowers individuals to make more informed decisions in various aspects of their lives. Remember that the simple question, "What is 60 percent of 20?" opens the door to a vast and incredibly useful mathematical concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 60 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.