What Is -8 To The Power Of 2
News Co
Apr 21, 2025 · 5 min read
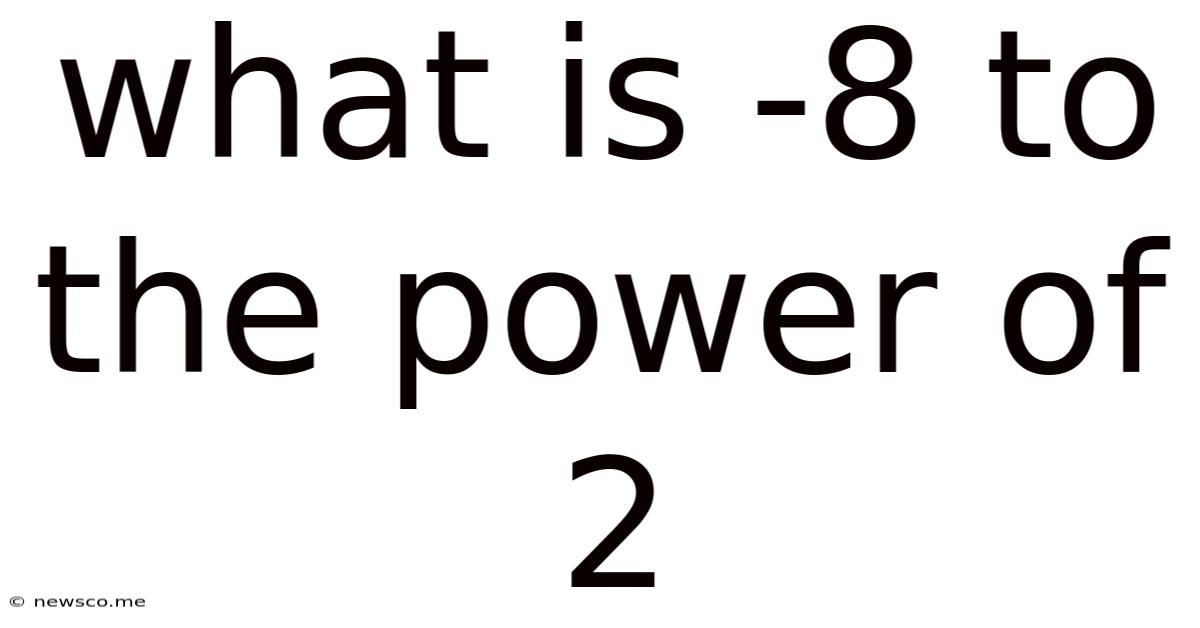
Table of Contents
What is -8 to the Power of 2? Unraveling the Mystery of Negative Bases and Exponents
The seemingly simple question, "What is -8 to the power of 2?", often trips up even those comfortable with basic arithmetic. The confusion arises from the interplay between negative numbers, exponents, and the order of operations. This article will delve deep into the intricacies of this mathematical concept, providing a clear and comprehensive explanation, complete with practical examples and related mathematical concepts.
Understanding Exponents
Before tackling the specific problem of (-8)² , let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates repeated multiplication. For instance, in the expression a<sup>n</sup>, 'a' is the base and 'n' is the exponent. This expression signifies that 'a' is multiplied by itself 'n' times.
- Example 1: 2³ = 2 × 2 × 2 = 8
- Example 2: 5² = 5 × 5 = 25
- Example 3: 10¹ = 10
The exponent dictates how many times the base is multiplied. A key point to remember is that the exponent applies only to the base directly adjacent to it.
The Role of Parentheses
Parentheses play a crucial role in mathematics, especially when dealing with negative numbers and exponents. They dictate the order of operations, ensuring that calculations are performed correctly. The placement of parentheses significantly impacts the outcome.
Let's contrast two scenarios:
Scenario 1: (-8)²
Here, the parentheses encompass the entire base, including the negative sign. This means the exponent applies to both the 8 and the negative sign. Therefore:
(-8)² = (-8) × (-8) = 64
Scenario 2: -8²
In this case, the parentheses are absent. The exponent 2 applies only to the base 8, not the negative sign. This means we perform the exponentiation first, then apply the negative sign. Therefore:
-8² = -(8 × 8) = -64
This subtle difference in notation leads to drastically different results. The presence or absence of parentheses completely changes the meaning and the final answer.
Order of Operations (PEMDAS/BODMAS)
The difference between (-8)² and -8² highlights the importance of adhering to the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). These acronyms provide a consistent framework for evaluating mathematical expressions.
In both (-8)² and -8², exponents take precedence over negation. However, the parentheses in (-8)² change the effective base to -8, resulting in a positive outcome. Without parentheses, as in -8², the negative sign remains separate and is applied after the exponentiation.
Expanding the Concept: Negative Exponents and Negative Bases
Let's broaden our understanding to incorporate negative exponents and negative bases.
Negative Exponents:
A negative exponent doesn't indicate a negative result; instead, it signifies a reciprocal.
- a<sup>-n</sup> = 1/a<sup>n</sup>
For example:
- 2<sup>-3</sup> = 1/2³ = 1/8
Negative Bases and Negative Exponents:
When dealing with both a negative base and a negative exponent, we combine the rules:
- (-a)<sup>-n</sup> = 1/(-a)<sup>n</sup>
For example:
- (-2)<sup>-3</sup> = 1/(-2)³ = 1/(-8) = -1/8
It's crucial to pay close attention to parentheses to avoid errors. The negative sign is part of the base when enclosed in parentheses.
Practical Applications and Real-World Examples
Understanding the nuances of negative bases and exponents isn't merely an academic exercise. These concepts have practical applications in various fields:
- Physics: Calculating acceleration, velocity, and other physical quantities often involve negative numbers and exponents.
- Finance: Compound interest calculations utilize exponents to determine the future value of investments. Negative numbers may represent losses or debts.
- Computer Science: In programming and algorithms, negative numbers and exponents are fundamental for data manipulation and calculations.
- Engineering: Many engineering applications, especially those involving exponential decay or growth, necessitate understanding these mathematical principles.
Common Mistakes and How to Avoid Them
Several common mistakes arise when working with negative bases and exponents:
- Ignoring Parentheses: This is the most frequent error, leading to incorrect results. Always ensure parentheses are correctly placed to clarify the order of operations.
- Misinterpreting Negative Exponents: Remember that a negative exponent represents a reciprocal, not a negative value.
- Incorrect Order of Operations: Failing to follow PEMDAS/BODMAS results in inaccurate calculations.
To avoid these mistakes:
- Use parentheses liberally: Enclose negative bases in parentheses, especially when raising them to a power.
- Break down complex expressions: Simplify expressions step by step, following the order of operations.
- Check your work: After completing a calculation, review your steps to ensure accuracy.
- Use a calculator cautiously: While calculators can be helpful, be sure you understand the rules and enter the expression correctly.
Advanced Concepts and Further Exploration
For those seeking a deeper understanding, consider exploring these related concepts:
- Complex Numbers: Extending the concept of exponents to include imaginary and complex numbers.
- Logarithms: The inverse function of exponentiation.
- Taylor and Maclaurin Series: Representing functions as infinite sums of powers.
Conclusion: Mastering Negative Bases and Exponents
Mastering the concept of negative bases and exponents is crucial for success in mathematics and various related fields. By understanding the importance of parentheses, adhering to the order of operations, and carefully applying the rules of exponents, you can confidently tackle even the most complex calculations involving negative numbers and powers. Remember, practice and careful attention to detail are key to achieving accuracy and building a strong foundation in mathematics. The seemingly straightforward question of "-8 to the power of 2" serves as a powerful reminder of the importance of precision and the nuances of mathematical notation. The answer, whether 64 or -64, depends entirely on how the expression is written and interpreted, underscoring the significance of a thorough understanding of mathematical principles.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is -8 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.