What Is 8 To The Power Of 3
News Co
Mar 23, 2025 · 6 min read
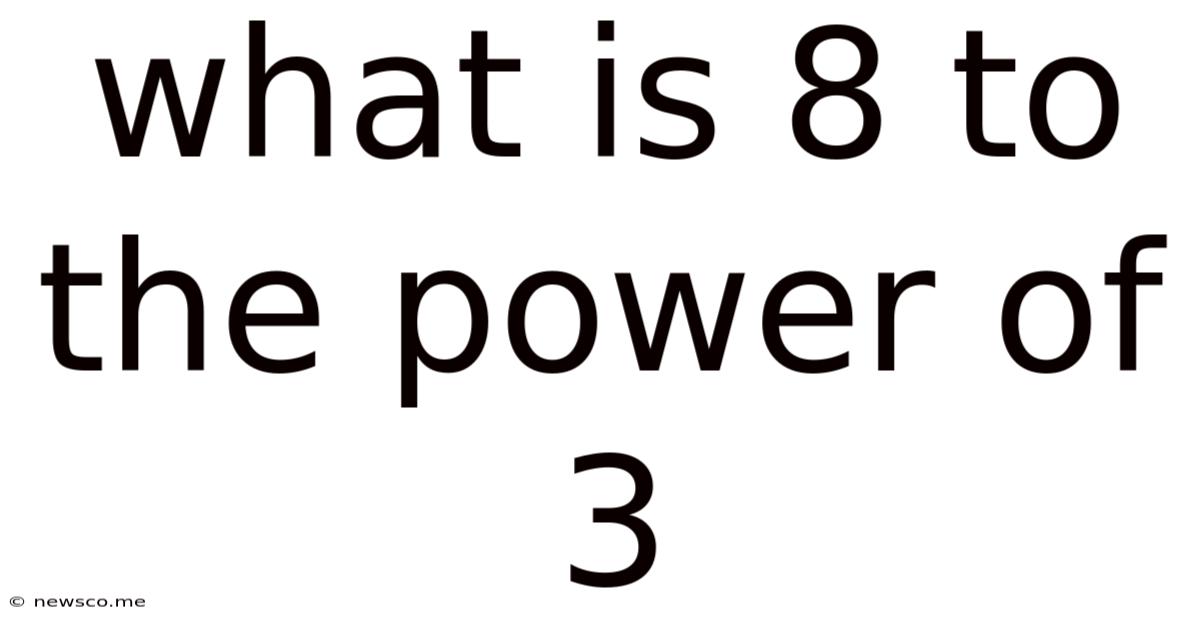
Table of Contents
What is 8 to the Power of 3? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 8 to the power of 3?" opens a door to a vast world of mathematical concepts and their practical applications. While the answer itself is straightforward (512), understanding the underlying principles of exponents, their properties, and their relevance across various fields provides a richer and more valuable learning experience. This article will explore this seemingly simple calculation in depth, examining the fundamental concepts, practical uses, and even some interesting historical context.
Understanding Exponents: The Fundamentals
Before we tackle 8 to the power of 3, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. It's represented by a superscript number placed to the right of the base. For instance, in the expression 8³, 8 is the base, and 3 is the exponent. This means 8 multiplied by itself three times: 8 × 8 × 8.
Key Terminology:
- Base: The number being multiplied repeatedly. In 8³, the base is 8.
- Exponent: The number indicating how many times the base is multiplied by itself. In 8³, the exponent is 3.
- Power: Another term for exponent. "8 to the power of 3" is the same as "8 cubed".
- Result: The final answer obtained after performing the multiplication. In this case, it's 512.
Simple Calculations:
Let's look at some simple examples to illustrate the concept:
- 2² = 2 × 2 = 4 (2 to the power of 2, or 2 squared)
- 3³ = 3 × 3 × 3 = 27 (3 to the power of 3, or 3 cubed)
- 5¹ = 5 (5 to the power of 1 – any number to the power of 1 is itself)
- 10⁰ = 1 (Any non-zero number to the power of 0 is 1)
- 4⁻¹ = 1/4 = 0.25 (Negative exponents represent reciprocals)
These examples demonstrate the fundamental principle of exponents: repeated multiplication.
Calculating 8 to the Power of 3
Now, let's return to our original question: What is 8 to the power of 3?
8³ = 8 × 8 × 8 = 64 × 8 = 512
Therefore, 8 to the power of 3 is 512.
Properties of Exponents: Expanding Our Understanding
Understanding the properties of exponents is crucial for efficient calculations and problem-solving. These properties allow us to manipulate exponential expressions and simplify complex calculations.
Product of Powers:
When multiplying two numbers with the same base, we add their exponents: aᵐ × aⁿ = aᵐ⁺ⁿ
For example: 2³ × 2² = 2³⁺² = 2⁵ = 32
Quotient of Powers:
When dividing two numbers with the same base, we subtract their exponents: aᵐ ÷ aⁿ = aᵐ⁻ⁿ
For example: 3⁵ ÷ 3² = 3⁵⁻² = 3³ = 27
Power of a Power:
When raising a power to another power, we multiply the exponents: (aᵐ)ⁿ = aᵐⁿ
For example: (2²)³ = 2²ˣ³ = 2⁶ = 64
Power of a Product:
When raising a product to a power, we raise each factor to that power: (ab)ⁿ = aⁿbⁿ
For example: (2 × 3)² = 2² × 3² = 4 × 9 = 36
Power of a Quotient:
When raising a quotient to a power, we raise both the numerator and the denominator to that power: (a/b)ⁿ = aⁿ/bⁿ
For example: (2/3)² = 2²/3² = 4/9
Practical Applications of Exponents
Exponents are far from being a purely theoretical concept. They have significant practical applications across numerous fields:
Science and Engineering:
- Compound Interest: Exponents are fundamental to calculating compound interest, where interest earned is added to the principal amount, and subsequent interest is calculated on the increased balance. The formula involves exponential growth.
- Exponential Decay: Radioactive decay, the process by which unstable atomic nuclei lose energy, follows an exponential decay model, described using exponential functions.
- Growth of Populations: The growth of populations (bacteria, animals, humans) can often be modeled using exponential functions, especially during periods of rapid growth.
- Physics and Chemistry: Many physical and chemical phenomena are described using exponential functions, including the behavior of waves, the decay of radioactive isotopes, and chemical reaction rates.
Computer Science:
- Binary System: Computers use the binary system (base 2), which relies heavily on exponents of 2 to represent numbers and data. Understanding exponents is vital for grasping how computers process information.
- Algorithm Complexity: The efficiency of algorithms is often expressed using Big O notation, which utilizes exponents to describe how the runtime or space requirements of an algorithm scale with input size.
- Data Structures: The analysis and optimization of data structures, such as trees and graphs, often involve exponential concepts.
Finance and Economics:
- Investment Growth: Understanding exponential growth is crucial for making informed investment decisions and assessing the long-term potential of investments.
- Economic Modeling: Exponential functions are frequently used in economic models to represent growth or decay processes, such as economic growth, inflation, or the decline of a resource.
Other Applications:
- Probability and Statistics: Exponents appear in many probability distributions, such as the binomial distribution and the Poisson distribution.
- Geometry: Exponents are essential in calculating volumes and areas of geometric shapes. For example, the volume of a cube is given by s³, where 's' is the length of a side.
- Cryptography: Exponents play a critical role in modern cryptography, particularly in public-key cryptography systems like RSA, which are used to secure online transactions and communications.
Beyond 8 to the Power of 3: Exploring Further
While we've answered the initial question, understanding 8³ is just the starting point. Exploring other exponents, particularly those involving larger numbers or fractions, and delving deeper into the properties of exponents will provide a more comprehensive understanding of this vital mathematical concept.
Exploring Larger Exponents: Consider calculating 8 to the power of 10, or even larger numbers. This highlights the rapid growth associated with exponents, demonstrating the power of exponential functions.
Exploring Fractional Exponents: Fractional exponents represent roots. For example, 8^(1/3) represents the cube root of 8, which is 2. This expands the concept beyond simple repeated multiplication to include the inverse operation of finding roots.
Exploring Negative Exponents: Negative exponents represent reciprocals. For example, 8⁻² is equivalent to 1/8². Understanding negative exponents expands the concept to include inverse relationships.
Conclusion: The Enduring Importance of Exponents
The seemingly simple question of "What is 8 to the power of 3?" has led us on a journey through the fascinating world of exponents. From understanding the basic principles of exponentiation to exploring their vast applications across various fields, we've seen the enduring importance of this concept. Mastering exponents isn't just about calculating numerical values; it's about understanding a powerful tool that helps us model, understand, and predict phenomena in the world around us. This fundamental mathematical concept continues to be essential in countless areas, from the intricacies of computer science to the complexities of financial markets and the wonders of the natural world. By building a solid foundation in this area, you equip yourself with a powerful tool for tackling challenges and exploring the complexities of the world around you.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 8 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.