What Is 80 Percent Of 40
News Co
Mar 23, 2025 · 5 min read
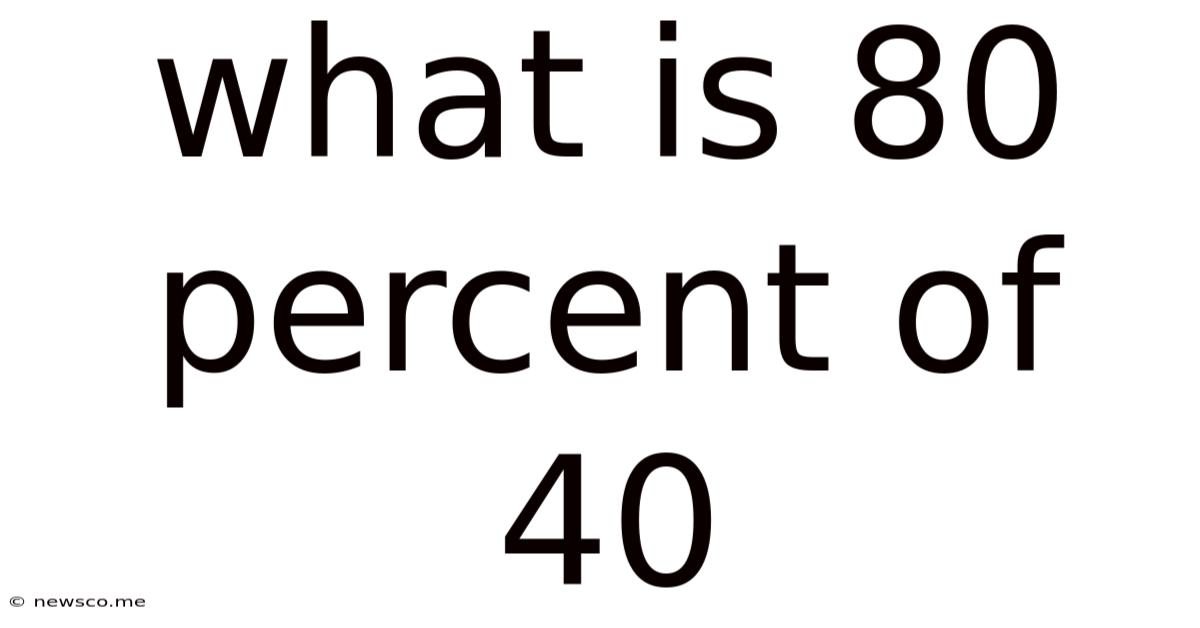
Table of Contents
What is 80 Percent of 40? A Deep Dive into Percentages and Their Applications
Finding 80 percent of 40 might seem like a simple arithmetic problem, easily solved with a calculator. However, understanding the underlying principles of percentages and their diverse applications extends far beyond this basic calculation. This article will delve into the solution, explore the concept of percentages in detail, and illustrate their relevance across various fields.
Calculating 80% of 40: The Simple Approach
The most straightforward way to calculate 80% of 40 is to convert the percentage to a decimal and then multiply:
80% = 80/100 = 0.8
0.8 * 40 = 32
Therefore, 80% of 40 is 32.
Understanding Percentages: A Fundamental Concept
Percentages are a way of expressing a number as a fraction of 100. They are used extensively to represent proportions, ratios, and changes in various contexts. The symbol "%" signifies "per hundred". Understanding percentages is crucial in numerous aspects of life, from calculating discounts and taxes to understanding financial reports and analyzing statistical data.
Key Concepts Related to Percentages:
-
Percentage Increase/Decrease: This refers to the change in a value expressed as a percentage of the original value. For example, a 10% increase in price means the new price is 110% of the original price.
-
Percentage Points: This is a measure of the absolute difference between two percentages. For instance, if interest rates rise from 5% to 8%, the increase is 3 percentage points, not 3%.
-
Percentage Change Formula: To calculate the percentage change between two values (new value and original value):
Percentage Change = [(New Value - Original Value) / Original Value] * 100 -
Finding the Original Value: If you know the percentage and the resulting value, you can calculate the original value. For example, if 20% of a number is 10, the original number is 10 / 0.2 = 50.
Real-World Applications of Percentages:
The applications of percentages are vast and far-reaching, impacting various sectors:
1. Finance and Business:
-
Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding interest rates is essential for making informed financial decisions.
-
Discounts and Sales: Retailers often offer discounts expressed as percentages to attract customers. Calculating the final price after a discount involves percentage calculations.
-
Profit Margins: Businesses determine their profit margin as a percentage of their revenue to assess profitability. Higher profit margins generally indicate better financial health.
-
Taxation: Taxes are usually calculated as a percentage of income, sales, or property value. Understanding tax percentages is crucial for accurate financial planning.
-
Investment Returns: Investors track their returns on investments as percentages to evaluate the performance of their portfolios.
2. Science and Statistics:
-
Data Analysis: Percentages are used extensively in statistical analysis to represent proportions within data sets. For example, survey results are often expressed as percentages.
-
Scientific Experiments: Percentages play a role in various scientific experiments, such as calculating the percentage of successful trials or the percentage of a substance in a solution.
-
Probability: Probabilities are often expressed as percentages to represent the likelihood of an event occurring.
3. Everyday Life:
-
Tipping: Many people calculate tips as a percentage of the bill amount in restaurants and other service industries.
-
Shopping: Understanding percentages is crucial for comparing prices and finding the best deals while shopping.
-
Cooking: Recipes often use percentages to indicate the proportion of ingredients.
-
Health and Fitness: Body fat percentage, progress in fitness goals, and nutritional information often utilize percentages.
Beyond the Basics: More Complex Percentage Problems
While calculating 80% of 40 is a straightforward exercise, more complex percentage problems require a deeper understanding of the concepts:
1. Finding the Percentage:
If you are given two numbers and need to find the percentage one represents of the other, use the following formula:
Percentage = (Part / Whole) * 100
For example, if 15 is part of a whole of 75, the percentage is (15/75) * 100 = 20%.
2. Increasing or Decreasing a Value by a Percentage:
To increase a value by a certain percentage, you can use this formula:
New Value = Original Value * (1 + Percentage Increase)
Similarly, to decrease a value by a certain percentage, you can use this formula:
New Value = Original Value * (1 - Percentage Decrease)
3. Successive Percentage Changes:
When dealing with multiple percentage changes, it's important to note that they don't simply add up. For example, a 10% increase followed by a 10% decrease does not result in the original value. Instead, you must calculate each change sequentially.
Practical Examples and Problem-Solving Strategies:
Let's look at a few more examples to solidify our understanding:
Example 1: A shirt originally costs $50. It's on sale for 20% off. What is the sale price?
Sale Price = $50 * (1 - 0.20) = $50 * 0.80 = $40
Example 2: A student scored 85 out of 100 on a test. What is their percentage score?
Percentage Score = (85 / 100) * 100 = 85%
Example 3: The population of a town increased by 15% to 6900. What was the original population?
Let x be the original population. Then:
x * 1.15 = 6900
x = 6900 / 1.15 = 6000
Conclusion: The Pervasiveness of Percentages
The seemingly simple calculation of 80% of 40 opens the door to a wide-ranging understanding of percentages and their importance in various fields. From daily transactions to complex financial models, percentages provide a concise and universally understood way to represent proportions and changes. Mastering the concepts of percentages equips individuals with essential skills for navigating the quantitative aspects of the world around them. This article has aimed to provide a comprehensive overview of the topic, highlighting both the basic calculations and more advanced applications, fostering a deeper comprehension of this fundamental mathematical concept. Remember to practice regularly to build confidence and fluency in working with percentages.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.