What Is 9/20 As A Percentage
News Co
Mar 21, 2025 · 5 min read
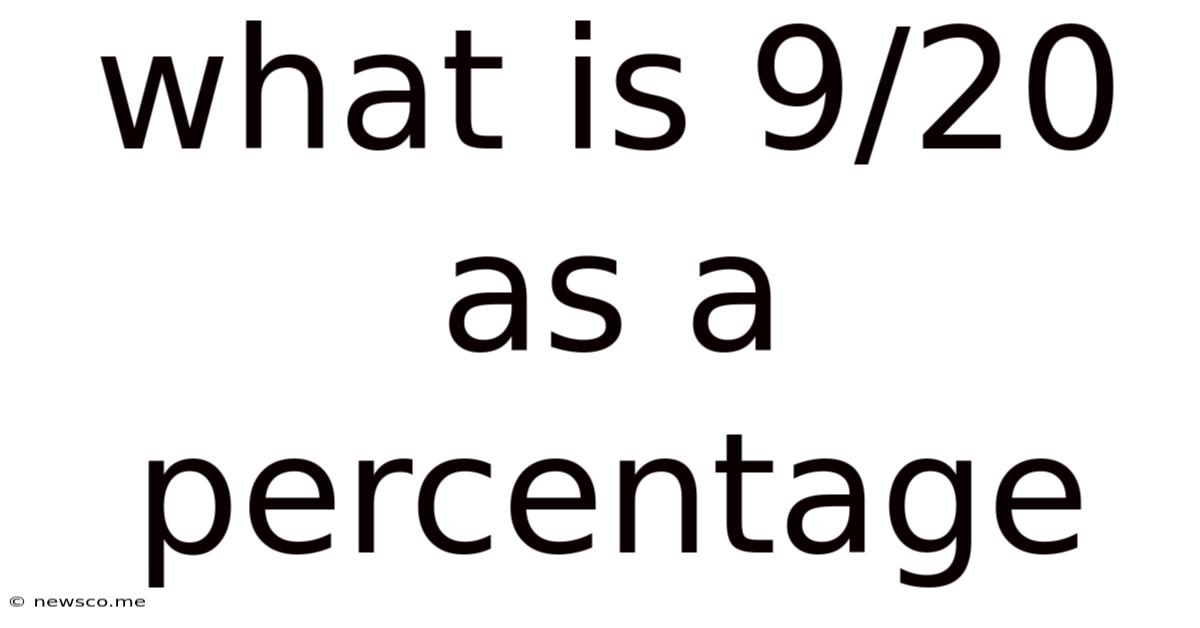
Table of Contents
What is 9/20 as a Percentage? A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in various fields. Understanding this process is crucial for everyday tasks, from calculating discounts and tax rates to interpreting data in financial reports and academic studies. This comprehensive guide will delve into the intricacies of converting 9/20 into a percentage, explaining the method step-by-step and exploring various related concepts. We'll also examine the practical applications of percentage calculations and address common misconceptions.
Understanding Fractions and Percentages
Before diving into the conversion, let's clarify the basic concepts of fractions and percentages.
Fractions
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts in the whole. For example, in the fraction 9/20, 9 is the numerator and 20 is the denominator. This means we have 9 parts out of a total of 20 equal parts.
Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of 100." Percentages are widely used to represent proportions, rates, and changes. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or 1/2.
Converting 9/20 to a Percentage: The Step-by-Step Method
To convert the fraction 9/20 into a percentage, we need to express it as a fraction with a denominator of 100. Here's the step-by-step process:
Step 1: Find the equivalent fraction with a denominator of 100.
To achieve this, we need to determine what number we must multiply the denominator (20) by to get 100. This is simple: 100 / 20 = 5.
Step 2: Multiply both the numerator and the denominator by the same number.
Since we multiplied the denominator by 5, we must also multiply the numerator by 5 to maintain the equivalence of the fraction. This gives us:
(9 * 5) / (20 * 5) = 45/100
Step 3: Express the fraction as a percentage.
Now that we have a fraction with a denominator of 100, we can easily express it as a percentage. The numerator (45) represents the percentage value. Therefore, 45/100 is equivalent to 45%.
Therefore, 9/20 as a percentage is 45%.
Alternative Method: Using Decimal Conversion
An alternative approach involves converting the fraction to a decimal first and then multiplying by 100 to obtain the percentage.
Step 1: Convert the fraction to a decimal.
To convert 9/20 to a decimal, we simply divide the numerator (9) by the denominator (20):
9 ÷ 20 = 0.45
Step 2: Multiply the decimal by 100.
Multiply the resulting decimal by 100 to express it as a percentage:
0.45 * 100 = 45%
This confirms that 9/20 is indeed equal to 45%.
Practical Applications of Percentage Calculations
Understanding how to convert fractions to percentages is invaluable in numerous real-world situations:
Finance and Economics:
- Calculating interest rates: Interest rates on loans, savings accounts, and investments are often expressed as percentages.
- Determining discounts and sales tax: Retail stores frequently advertise discounts as percentages (e.g., 20% off). Sales tax is also calculated as a percentage of the purchase price.
- Analyzing financial statements: Financial reports often present data as percentages to facilitate comparisons and trend analysis. For example, profit margins, return on investment (ROI), and debt-to-equity ratios are typically expressed as percentages.
Science and Statistics:
- Representing proportions and ratios: Percentages are used to represent proportions within datasets, such as the percentage of a population with a certain characteristic.
- Interpreting experimental results: Scientific experiments often involve calculating percentages to analyze the results and draw conclusions.
- Presenting statistical data: Percentages are a common way to present statistical data in a clear and easily understandable format.
Everyday Life:
- Calculating tips and gratuities: Restaurant patrons often calculate tips as a percentage of the bill (e.g., 15% or 20%).
- Understanding survey results: Surveys frequently report results as percentages, showing the proportion of respondents who selected each option.
- Comparing prices and values: Percentages are helpful for comparing prices and values of different products or services.
Common Misconceptions about Percentages
While percentage calculations are relatively straightforward, several common misconceptions can lead to errors:
- Confusing percentages with decimal values: Remember that percentages are always out of 100. A decimal value must be multiplied by 100 to be expressed as a percentage.
- Incorrectly adding or subtracting percentages: Percentages cannot be directly added or subtracted unless they refer to the same base value. For example, a 10% increase followed by a 10% decrease does not result in the original value.
- Misinterpreting percentage changes: Percentage changes are relative to the original value. A 10% increase on 100 is 110, but a 10% decrease on 200 is 180. The magnitude of the percentage change is the same (10%), but the absolute change differs.
Conclusion: Mastering Percentage Conversions
The ability to convert fractions to percentages is a vital skill that extends far beyond the classroom. Whether you're navigating financial transactions, interpreting data, or solving everyday problems, a solid understanding of percentages will empower you to make informed decisions and communicate effectively. By mastering this fundamental concept and avoiding common misconceptions, you'll gain confidence in your mathematical abilities and unlock a world of opportunities. Remember that practice is key to solidifying your understanding. Try converting different fractions to percentages to enhance your skills and build fluency. The simple process outlined above, combined with consistent practice, will enable you to confidently tackle any percentage calculation you encounter.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 9/20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.