What Is 9 Percent Of 20
News Co
Apr 19, 2025 · 5 min read
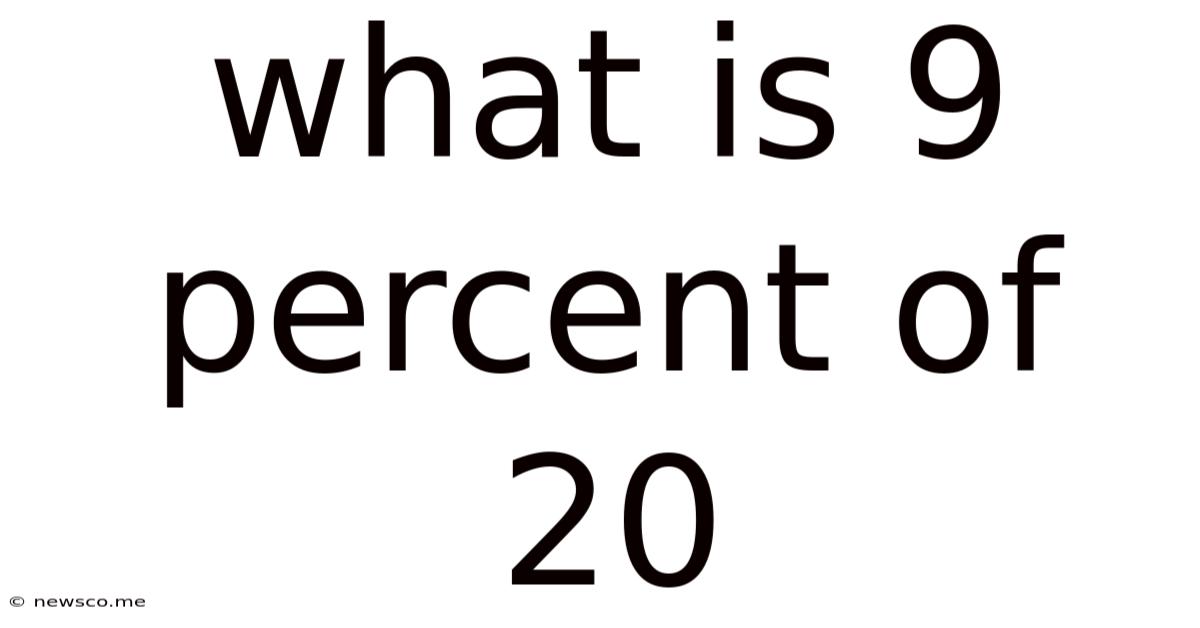
Table of Contents
What is 9 Percent of 20? A Deep Dive into Percentage Calculations
This seemingly simple question, "What is 9 percent of 20?", opens the door to a fascinating exploration of percentage calculations, their real-world applications, and the underlying mathematical principles. While the answer itself is easily obtained using a calculator or simple arithmetic, understanding the why behind the calculation is crucial for anyone seeking to master percentages and apply them effectively in various contexts.
Understanding Percentages: The Foundation
Before we delve into the specifics of calculating 9% of 20, let's establish a solid understanding of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 9% can be interpreted as 9 out of 100, or 9/100.
This fractional representation is key to understanding percentage calculations. Any percentage can be easily converted into a decimal by dividing it by 100. For instance, 9% becomes 0.09 (9 ÷ 100 = 0.09). This decimal representation is often the most convenient form for performing calculations.
Calculating 9% of 20: Three Approaches
There are several ways to calculate 9% of 20. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward approach. As we established, 9% is equivalent to 0.09. To find 9% of 20, we simply multiply 20 by 0.09:
20 x 0.09 = 1.8
Therefore, 9% of 20 is 1.8.
Method 2: Using Fractions
We can also solve this using the fractional representation of 9%. Remember, 9% is the same as 9/100. To find 9% of 20, we multiply 20 by 9/100:
20 x (9/100) = 180/100 = 1.8
Again, the answer is 1.8. This method highlights the direct relationship between percentages, fractions, and decimals.
Method 3: Proportion Method
This method involves setting up a proportion. We know that 9% is 9 out of 100. We can set up a proportion to find the equivalent value out of 20:
9/100 = x/20
To solve for x (which represents 9% of 20), we cross-multiply:
100x = 9 * 20 100x = 180 x = 180/100 x = 1.8
Once again, the answer is 1.8. This approach is particularly helpful when dealing with more complex percentage problems.
Real-World Applications: Where Percentages Matter
Understanding percentage calculations isn't just an academic exercise; it's a vital skill with countless real-world applications. Consider the following examples:
-
Sales and Discounts: Stores frequently advertise discounts as percentages. If a $20 item is discounted by 9%, the calculation we've just performed tells us the discount amount is $1.80.
-
Taxes: Sales tax is another common application. If the sales tax rate is 9%, calculating the tax on a $20 purchase involves the same percentage calculation.
-
Tips and Gratuities: Calculating a tip at a restaurant often involves percentages. A 9% tip on a $20 meal would be $1.80.
-
Interest Rates: Understanding percentages is crucial for comprehending interest rates on loans, savings accounts, and investments.
-
Statistical Analysis: Percentages are fundamental in various statistical analyses, allowing for the representation of data as proportions and facilitating comparisons.
-
Financial Reporting: Financial statements heavily rely on percentages to express key metrics like profit margins, expense ratios, and return on investment.
-
Scientific Research: Many scientific studies utilize percentages to represent data and analyze results.
Expanding Your Percentage Skills: Beyond the Basics
While calculating 9% of 20 provides a foundational understanding of percentage calculations, there are many more complex scenarios you may encounter. Here are some areas to explore:
-
Calculating Percentage Increase or Decrease: This involves finding the percentage change between two values. For instance, if a value increases from 20 to 22, what's the percentage increase?
-
Finding the Original Value: If a value is increased by 9% to become 21.8, what was the original value?
-
Working with Multiple Percentages: What if you need to calculate consecutive percentage increases or decreases?
-
Percentage Points vs. Percentage Change: It's crucial to differentiate between these two concepts, as they represent different things.
Mastering these more advanced techniques requires a deeper understanding of algebraic principles and problem-solving strategies. Practice is key to becoming proficient. Work through various examples, starting with simple problems and gradually increasing the complexity. Online resources, textbooks, and even educational apps can provide ample practice opportunities.
The Importance of Accuracy and Precision in Percentage Calculations
Accuracy and precision are paramount when working with percentages, especially in financial and scientific applications where even small errors can have significant consequences. Always double-check your calculations and use appropriate tools (calculators, spreadsheets) to minimize the risk of errors. Understanding significant figures and rounding rules is also essential to ensure the precision of your results aligns with the context of the problem.
Conclusion: Mastering Percentages for a Better Understanding of the World
Understanding percentages is a fundamental skill applicable to numerous aspects of life. From everyday shopping to complex financial analyses, the ability to confidently and accurately perform percentage calculations is invaluable. While the seemingly simple problem of finding 9% of 20 provides a starting point, it encourages a deeper exploration into the world of percentages, their applications, and the mathematical principles that underpin them. By mastering these concepts, you equip yourself with a valuable tool for navigating and understanding the quantitative aspects of the world around you. So, the next time you encounter a percentage problem, remember the simple yet powerful techniques discussed here, and approach it with confidence and precision.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 9 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.