What Is 90 Percent Of 20
News Co
Mar 19, 2025 · 5 min read
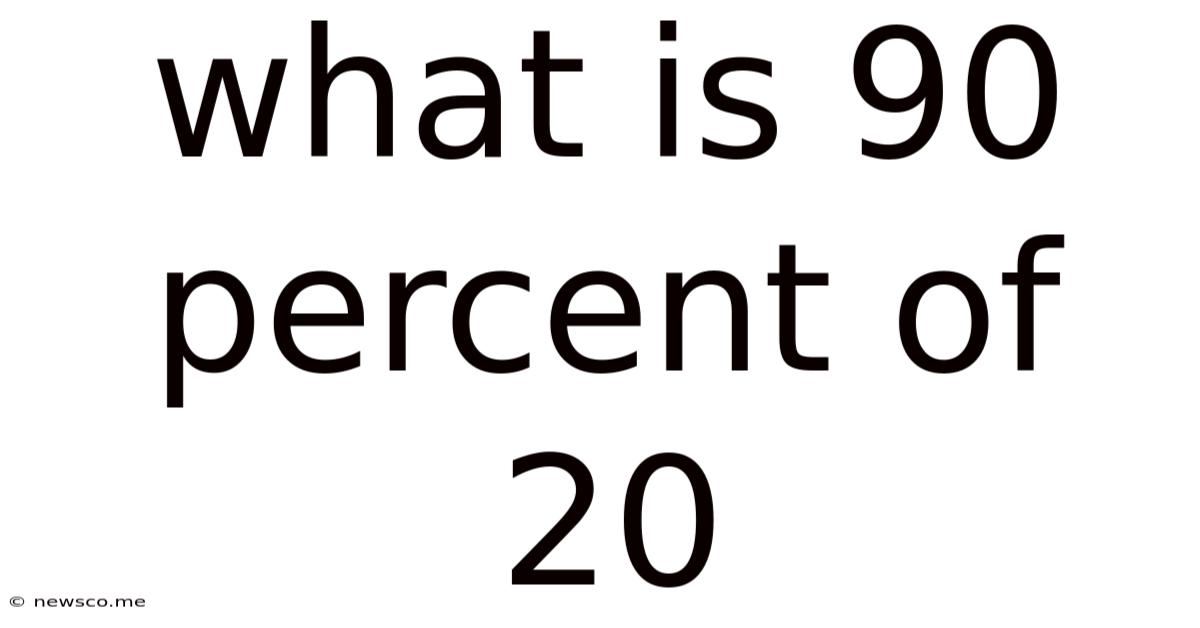
Table of Contents
What is 90 Percent of 20? A Deep Dive into Percentages and Their Applications
Finding 90 percent of 20 might seem like a simple arithmetic problem, suitable only for elementary school. However, understanding the underlying concepts and the various methods to solve this problem opens the door to a much broader understanding of percentages, their applications in everyday life, and their importance in various fields. This article will not only answer the question directly but also explore the topic in depth, offering multiple approaches to solving percentage problems and showcasing their relevance in real-world scenarios.
Understanding Percentages: The Building Blocks
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100." For example, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5.
Percentages are used extensively to represent proportions, ratios, and changes in various contexts. From calculating discounts in a store to understanding economic growth rates or analyzing survey results, percentages provide a standardized and easily understandable way to convey numerical information.
Calculating 90 Percent of 20: Three Methods
Now, let's tackle the primary question: What is 90 percent of 20? We can solve this using three different methods:
Method 1: Using the Fraction Method
We can convert the percentage to a fraction and then multiply it by the number. 90% can be written as the fraction 90/100, which simplifies to 9/10. Therefore, 90% of 20 is calculated as:
(9/10) * 20 = 18
This method is straightforward and easy to understand, especially for those who are comfortable working with fractions.
Method 2: Using Decimal Conversion
Alternatively, we can convert the percentage to a decimal. 90% is equivalent to 0.9 (because 90/100 = 0.9). The calculation then becomes:
0.9 * 20 = 18
This method is often preferred for its simplicity when using calculators or performing calculations with larger numbers.
Method 3: Using Proportions
A third approach involves setting up a proportion. We can represent the problem as:
x/20 = 90/100
To solve for x (which represents 90% of 20), we cross-multiply:
100x = 90 * 20
100x = 1800
x = 1800/100
x = 18
This method provides a more formal mathematical approach and can be particularly helpful in solving more complex percentage problems.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world situations. Here are some examples:
1. Shopping and Discounts:
Imagine you find a shirt priced at $20 with a 90% discount. Using the methods discussed above, you can quickly determine that the discount is $18 (90% of $20), and the final price you pay is $2.
2. Sales and Commission:
Salespeople often earn commissions based on a percentage of their sales. If a salesperson earns a 10% commission on sales and sells $200 worth of goods, their commission would be $20 (10% of $200). Understanding percentage calculations allows for accurate commission calculations.
3. Financial Analysis:
In finance, percentages are essential for analyzing growth rates, interest calculations, and investment returns. For example, if an investment grows by 20% in one year, and you want to calculate how much it will grow if it continues at that rate for another year, you'll need to apply percentage calculations correctly.
4. Grade Calculations:
In education, percentages are fundamental to calculating grades. If a student scores 18 out of 20 on a test, their score is 90%. Understanding percentages helps interpret scores and understand performance levels.
5. Data Analysis and Statistics:
Percentages are ubiquitous in data analysis and statistics. They are used to represent proportions within datasets, visualize trends, and make comparisons between different groups. For instance, if a survey shows that 90% of respondents prefer a particular product, this percentage is used to draw inferences about market preferences.
6. Tax Calculations:
Many countries use a percentage-based tax system, such as sales tax or income tax. Understanding percentages allows for accurate calculation of taxes owed.
Beyond the Basics: Advanced Percentage Problems
While finding 90% of 20 is a straightforward calculation, many percentage problems involve more intricate steps. Here are some examples of more advanced scenarios:
-
Calculating the original value: If a product is discounted by 10% and now costs $18, how much did it originally cost? This requires working backwards using the percentage.
-
Calculating percentage increase or decrease: If a value increases from 20 to 25, what is the percentage increase? This requires calculating the difference and expressing it as a percentage of the original value.
-
Compound percentages: Calculating percentage growth over multiple periods, where the percentage is applied to the new value each period, as with compound interest.
-
Percentage change after multiple percentage changes: For example, a price rises by 10%, then falls by 10%. The final price isn't the same as the original price because the 10% decrease is calculated on the higher price.
Mastering Percentages: Tips and Resources
Mastering percentage calculations requires practice and a strong understanding of fundamental mathematical concepts. Here are some tips to improve your skills:
-
Practice regularly: Solve a variety of percentage problems, starting with simple ones and gradually progressing to more complex ones.
-
Use different methods: Familiarize yourself with various methods for solving percentage problems to find the approach that suits you best.
-
Utilize online resources: Many websites and online calculators can help you practice and check your answers.
-
Break down complex problems: Divide complex percentage problems into smaller, more manageable steps.
-
Visual aids: Use diagrams or charts to help visualize the problem and understand the relationships between quantities.
Conclusion
While the answer to "What is 90 percent of 20?" is simply 18, the journey to understanding the calculation highlights the broader importance and widespread applications of percentages in various fields. From everyday shopping to complex financial modeling, a strong grasp of percentage calculations is a valuable skill that transcends the realm of elementary arithmetic. By mastering the concepts and practicing regularly, you can confidently tackle a wide range of percentage problems and apply them effectively in diverse real-world scenarios. Remember to practice consistently and explore various methods to solidify your understanding of percentages and their vast applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 90 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.