What Is A 20 Out Of 25 As A Percentage
News Co
May 07, 2025 · 5 min read
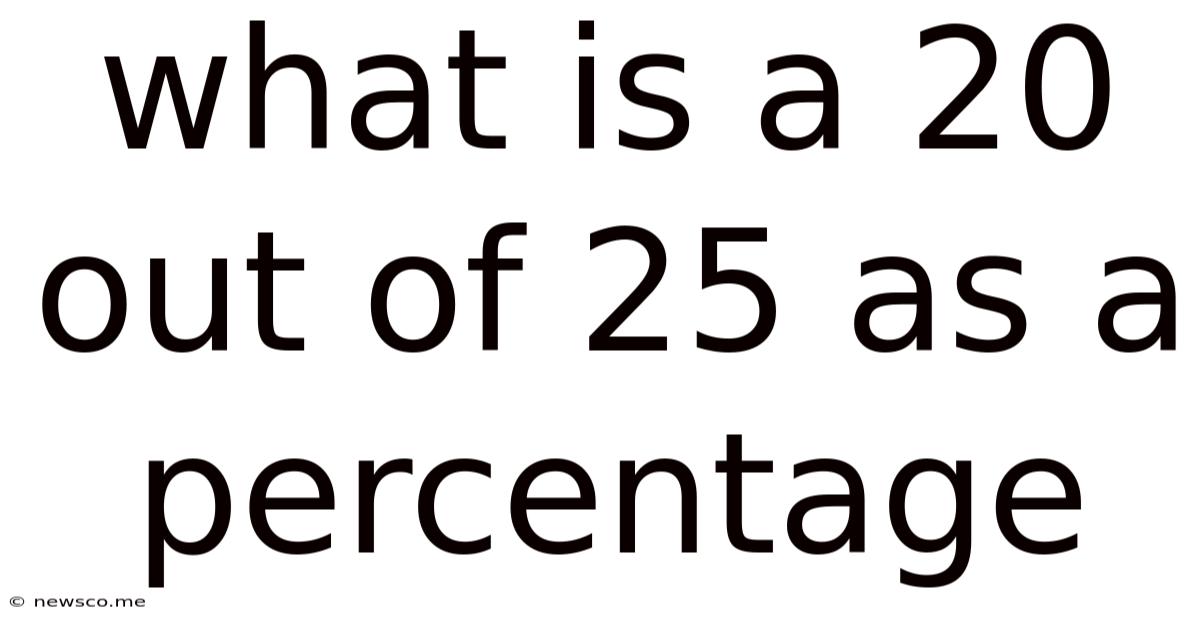
Table of Contents
What is a 20 out of 25 as a Percentage? A Comprehensive Guide
Calculating percentages is a fundamental skill with wide-ranging applications, from academic assessments to financial transactions. Understanding how to convert fractions into percentages is crucial for interpreting data and making informed decisions. This comprehensive guide will delve into the specifics of calculating "20 out of 25 as a percentage," explaining the process step-by-step and offering further insights into percentage calculations.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred." The symbol used to represent percentages is the percent sign, "%". Percentages are used extensively to represent proportions, rates, and changes in various contexts.
Calculating 20 out of 25 as a Percentage
To calculate 20 out of 25 as a percentage, we need to follow these simple steps:
Step 1: Set up the Fraction
The first step is to represent the given information as a fraction. "20 out of 25" can be written as the fraction 20/25.
Step 2: Convert the Fraction to a Decimal
To convert the fraction to a decimal, we divide the numerator (the top number) by the denominator (the bottom number):
20 ÷ 25 = 0.8
Step 3: Convert the Decimal to a Percentage
To convert the decimal to a percentage, we multiply the decimal by 100 and add the percent sign:
0.8 x 100 = 80%
Therefore, 20 out of 25 is equal to 80%.
Alternative Calculation Method: Using Proportions
Another method to calculate percentages involves using proportions. This method is particularly useful when dealing with more complex scenarios. We can set up a proportion:
20/25 = x/100
Where 'x' represents the percentage we want to find. To solve for x, we cross-multiply:
25x = 2000
x = 2000 ÷ 25
x = 80
Therefore, x = 80%, confirming our previous calculation.
Practical Applications of Percentage Calculations
The ability to calculate percentages has numerous practical applications in various fields:
1. Academic Performance
Calculating grades and scores frequently involves percentages. A student scoring 20 out of 25 on a test achieves an 80% grade. This allows for easy comparison of performance across different tests or assignments, even if they have different total marks.
2. Financial Calculations
Percentages are fundamental in financial calculations, including interest rates, discounts, taxes, and profit margins. Understanding percentage changes helps in analyzing financial growth or decline. For instance, a 20% discount on a $100 item means a saving of $20.
3. Data Analysis and Statistics
Percentages are widely used in data analysis and statistics to represent proportions and trends within datasets. For example, if a survey shows 20 out of 25 respondents prefer a certain product, it indicates an 80% preference rate.
4. Business and Economics
Businesses utilize percentages extensively for various purposes, including calculating profit margins, market share, growth rates, and return on investment (ROI). Understanding percentage changes is crucial for strategic decision-making.
5. Everyday Life
Percentage calculations permeate our daily lives. We encounter them when calculating tips in restaurants, determining sales tax, understanding discounts, interpreting nutritional information on food labels, and much more.
Common Percentage Calculation Mistakes to Avoid
While calculating percentages is relatively straightforward, several common mistakes can lead to incorrect results. Being aware of these pitfalls can improve accuracy:
-
Incorrect Fraction Setup: Ensure the correct fraction is set up. The part being considered should be the numerator, and the total should be the denominator. Confusing these can lead to inaccurate results.
-
Division Errors: Errors in division can significantly impact the final percentage. Double-check your calculations, especially when dealing with decimals. Using a calculator can minimize the risk of errors.
-
Multiplication Errors: When converting the decimal to a percentage, ensure you multiply by 100, not by 10 or another factor. A simple mistake here can produce an incorrect result.
-
Incorrect Interpretation: Always carefully interpret the percentage in context. Understanding what the percentage represents is crucial for drawing accurate conclusions.
Advanced Percentage Calculations: Percentage Increase and Decrease
Beyond basic percentage calculations, understanding percentage increases and decreases is important for various real-world scenarios:
Percentage Increase:
Calculating a percentage increase involves finding the difference between two values and expressing this difference as a percentage of the original value. For example, if a value increases from 20 to 25, the percentage increase is calculated as follows:
- Find the difference: 25 - 20 = 5
- Divide the difference by the original value: 5 ÷ 20 = 0.25
- Multiply the result by 100 to express it as a percentage: 0.25 x 100 = 25%
Therefore, the value increased by 25%.
Percentage Decrease:
Calculating a percentage decrease follows a similar process but with a subtraction in step 1. If a value decreases from 25 to 20, the percentage decrease is:
- Find the difference: 25 - 20 = 5
- Divide the difference by the original value: 5 ÷ 25 = 0.2
- Multiply the result by 100 to express it as a percentage: 0.2 x 100 = 20%
Therefore, the value decreased by 20%.
Conclusion
Calculating percentages is a crucial skill applicable in numerous contexts. Understanding the process of converting fractions to percentages, along with avoiding common mistakes, ensures accurate results. Mastering percentage calculations empowers individuals to interpret data effectively, make informed decisions, and navigate various aspects of academic, financial, and daily life situations confidently. The calculation of 20 out of 25 as 80% serves as a fundamental example that showcases the broader implications of this essential mathematical skill. With practice and understanding of the underlying principles, accurate and efficient percentage calculations become second nature.
Latest Posts
Latest Posts
-
Cuanto Es 40 Grados En Estados Unidos
May 08, 2025
-
What Is The Lcm For 5 6 7
May 08, 2025
-
Differentiate To The Power Of X
May 08, 2025
-
How Much Is 12000 Pounds In American Money
May 08, 2025
-
Irrational Numbers Are Closed Under Division
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is A 20 Out Of 25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.