What Is A Constant Term In A Polynomial
News Co
Apr 06, 2025 · 5 min read
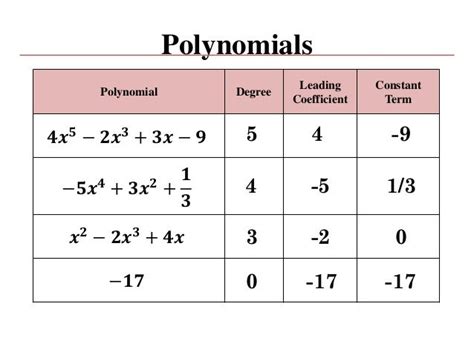
Table of Contents
What is a Constant Term in a Polynomial? A Comprehensive Guide
Understanding polynomial expressions is fundamental in algebra and numerous applications across various fields like science, engineering, and computer science. Within the structure of a polynomial, the constant term plays a significant role, often overlooked despite its importance. This comprehensive guide will delve deep into the definition, identification, and significance of the constant term in a polynomial, equipping you with a solid understanding of this key algebraic concept.
Defining the Constant Term
A polynomial is an expression consisting of variables (often represented by x, y, z, etc.) raised to non-negative integer powers, combined with constants using addition, subtraction, and multiplication. The general form of a polynomial in one variable, x, is:
aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₂x² + a₁x + a₀
Where:
aₙ, aₙ₋₁, ..., a₂, a₁, a₀are the coefficients, which are real numbers.nis a non-negative integer, representing the degree of the polynomial.xis the variable.
The constant term in a polynomial is the term that does not contain any variables. It's simply the coefficient a₀ in the general form above. This term remains constant regardless of the value assigned to the variable(s).
In simpler terms: The constant term is the number that's added or subtracted at the end of the polynomial. It's the part that doesn't change when the variable changes.
Identifying the Constant Term in Different Polynomial Types
Identifying the constant term is straightforward in many cases, but understanding its presence in various polynomial forms is crucial. Let's explore a few examples:
1. Polynomials in One Variable:
- Example 1: 3x² + 5x - 7. The constant term is -7.
- Example 2: 2x⁴ - 6x + 11. The constant term is 11.
- Example 3: x³ + 2x². The constant term is 0. (It's important to note that the absence of a constant term means the constant term is 0.)
2. Polynomials in Multiple Variables:
- Example 1: 2xy + 3x - 4y + 9. The constant term is 9.
- Example 2: x²y² - 5xy + 2x - 8. The constant term is -8.
- Example 3: 3x²z + 7yz. The constant term is 0.
3. Special Cases:
- Constant Polynomials: A polynomial consisting only of a constant term, e.g., 5, -2, or π. The constant term is the polynomial.
- Zero Polynomial: A polynomial where all coefficients are zero. This also has a constant term of 0.
The Significance of the Constant Term
The constant term holds several important properties and applications:
1. y-intercept of a Polynomial Function:
When a polynomial is considered as a function, the constant term represents the y-intercept. This is the point where the graph of the polynomial intersects the y-axis. The x-coordinate is always 0. When you substitute x = 0 into the polynomial, all terms with x vanish, leaving only the constant term.
2. Remainder Theorem:
The remainder theorem states that when a polynomial P(x) is divided by (x - c), the remainder is P(c). This implies that substituting the value 'c' into the polynomial gives the remainder. Interestingly, if 'c' is 0, the remainder is simply the constant term.
3. Factorization and Roots:
In some factorization techniques, understanding the constant term's relationship to the roots of the polynomial can be beneficial. The product of the roots of a polynomial is related to the constant term (and the leading coefficient). This relationship is particularly useful when dealing with quadratic equations.
4. Applications in Various Fields:
Constant terms appear across diverse fields:
- Physics: In physics equations describing motion or other phenomena, the constant term might represent an initial condition or a fundamental constant.
- Engineering: Constant terms often feature in design equations, representing fixed parameters or offsets.
- Computer Science: In algorithms and data structures, constants appear frequently, influencing the efficiency or complexity of the algorithm.
- Economics: In economic models, constant terms might represent fixed costs or baseline values.
Advanced Concepts and Further Exploration
While the basic identification of a constant term is straightforward, deeper understanding involves exploring more advanced concepts:
1. Polynomial Long Division:
In polynomial long division, the constant term plays a role in determining the remainder. When dividing a polynomial by another polynomial, the constant term of the remainder is obtained by a systematic process.
2. Partial Fraction Decomposition:
In partial fraction decomposition, where a rational function is broken down into simpler fractions, the constant terms of the resulting fractions are often determined by solving a system of equations derived from equating coefficients.
3. Numerical Analysis:
In numerical methods for solving polynomials, the constant term contributes to the overall solution. Techniques like the Newton-Raphson method involve iterative calculations where the constant term affects the convergence of the process.
4. Abstract Algebra:
In abstract algebra, polynomials are studied in a more general setting, extending to fields other than real numbers. The constant term, even in these abstract settings, retains its significance within the algebraic structures.
Conclusion: The Unsung Hero of Polynomial Expressions
The constant term in a polynomial might seem like a minor detail at first glance, a simple number tacked onto the end of a longer expression. However, a closer examination reveals its significant role in various aspects of algebra and its applications. From representing the y-intercept of a function to impacting factorization and even playing a role in advanced mathematical concepts, the constant term is an integral component of polynomials. Understanding its properties and significance allows for a more comprehensive and nuanced understanding of this fundamental algebraic structure, ultimately enhancing your ability to work with and interpret polynomial expressions effectively in diverse contexts. Therefore, don't overlook the seemingly insignificant constant term—it holds more power than you might initially realize.
Latest Posts
Latest Posts
-
Is 12 Prime Or Composite Number
Apr 07, 2025
-
1 4 Mile Is How Many Feet
Apr 07, 2025
-
Ratio Word Problems Worksheets With Answers
Apr 07, 2025
-
What Is The Square Root Of 4096
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Is A Constant Term In A Polynomial . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
