What Is A Factor Of 57
News Co
Apr 06, 2025 · 6 min read
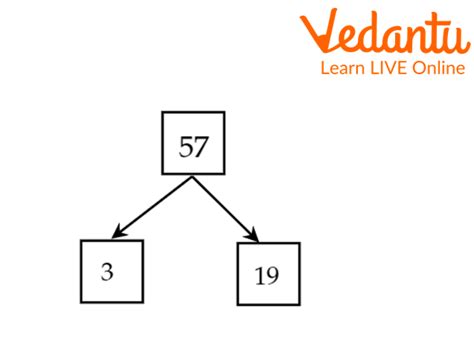
Table of Contents
What is a Factor of 57? A Deep Dive into Number Theory
Understanding factors is fundamental to grasping number theory and algebra. This article will explore the concept of factors, specifically focusing on the factors of 57. We'll delve into definitions, methods for finding factors, and explore the broader implications of factor analysis within mathematics.
Understanding Factors and Divisibility
Before we pinpoint the factors of 57, let's establish a clear understanding of what a factor is. A factor (or divisor) of a number is a whole number that divides evenly into that number without leaving a remainder. In simpler terms, if you divide a number by its factor, the result is another whole number.
For example, 2 is a factor of 10 because 10 divided by 2 equals 5 (a whole number). Similarly, 1, 2, 5, and 10 are all factors of 10.
Divisibility is closely related to the concept of factors. A number is divisible by another number if the result of the division is a whole number. Therefore, 10 is divisible by 2, 5, and 10. The factors of a number are all the numbers that divide it evenly.
Finding the Factors of 57: A Step-by-Step Approach
Now, let's determine the factors of 57. We'll employ a systematic approach:
-
Start with 1 and the number itself: Every number has 1 and itself as factors. Thus, 1 and 57 are factors of 57.
-
Check for prime factors: A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Let's see if any prime numbers divide 57 evenly. We can begin testing prime numbers sequentially: 2, 3, 5, 7, etc.
- 57 is not divisible by 2 (it's not an even number).
- 57 is divisible by 3 (57 ÷ 3 = 19). Therefore, 3 is a factor of 57.
-
Identify the remaining factor: Since 3 is a factor and 57 ÷ 3 = 19, this means 19 is also a factor of 57.
-
Complete the factor list: We've found all the factors: 1, 3, 19, and 57.
Therefore, the factors of 57 are 1, 3, 19, and 57.
Prime Factorization and its Significance
The process of finding the prime factors of a number is called prime factorization. It's a fundamental concept in number theory. Prime factorization expresses a number as a product of its prime factors. In the case of 57, the prime factorization is 3 x 19.
Prime factorization has several significant applications:
- Simplifying fractions: Prime factorization helps simplify fractions to their lowest terms.
- Finding the greatest common divisor (GCD): The GCD of two or more numbers is the largest number that divides all of them evenly. Prime factorization simplifies the process of finding the GCD.
- Finding the least common multiple (LCM): The LCM of two or more numbers is the smallest number that is a multiple of all of them. Prime factorization facilitates finding the LCM.
- Cryptography: Prime factorization plays a crucial role in many cryptographic systems, such as RSA encryption.
Exploring Divisibility Rules: A Shortcut for Factor Identification
Divisibility rules provide quick methods for determining whether a number is divisible by certain smaller numbers without performing long division. These rules can significantly speed up the process of finding factors. Let's examine some relevant divisibility rules for 57:
-
Divisibility by 2: A number is divisible by 2 if its last digit is an even number (0, 2, 4, 6, or 8). Since the last digit of 57 is 7 (odd), 57 is not divisible by 2.
-
Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3. The sum of the digits of 57 (5 + 7 = 12) is divisible by 3 (12 ÷ 3 = 4). Therefore, 57 is divisible by 3.
-
Divisibility by 5: A number is divisible by 5 if its last digit is either 0 or 5. Since the last digit of 57 is 7, 57 is not divisible by 5.
Factors, Multiples, and Their Relationship
It's crucial to differentiate between factors and multiples. While factors divide a number evenly, multiples are the result of multiplying a number by another whole number.
For instance, the multiples of 57 are 57, 114, 171, 228, and so on. Observe that the factors of 57 (1, 3, 19, 57) are related to its multiples. Each factor is a divisor of the multiples of 57.
Applications of Factors in Real-World Scenarios
The concept of factors extends beyond the realm of theoretical mathematics and finds practical applications in various real-world scenarios:
-
Geometry: Factors are essential in calculating areas and volumes of geometric shapes. For example, determining the dimensions of a rectangular plot of land with a given area requires finding factors of the area.
-
Data organization: Factors are useful in organizing data into rows and columns, such as arranging items in a grid or creating spreadsheets. The number of rows and columns must be factors of the total number of items.
-
Scheduling: Factors can be used to optimize scheduling problems. For instance, dividing tasks amongst team members or organizing shifts based on factors of the total available time.
-
Music: Musical harmony involves frequencies that are often multiples or factors of each other.
Advanced Concepts Related to Factors
Let's touch upon some more advanced concepts associated with factors:
-
Greatest Common Factor (GCF): The GCF of two or more numbers is the largest number that divides all of them without leaving a remainder.
-
Least Common Multiple (LCM): The LCM of two or more numbers is the smallest number that is a multiple of all of them.
-
Euclidean Algorithm: The Euclidean algorithm is an efficient method for computing the GCF of two numbers.
-
Factor Theorem: In algebra, the factor theorem states that a polynomial has a factor (x-a) if and only if f(a) = 0.
Conclusion: The Importance of Understanding Factors
Understanding factors is a cornerstone of mathematical literacy. This article delves into the definition, identification, and application of factors, specifically focusing on the factors of 57. We explored methods to find factors, including prime factorization, and touched upon divisibility rules as useful shortcuts. We also examined the relationship between factors and multiples and highlighted the practical applications of factors in various fields. A solid grasp of factors provides a foundation for more advanced mathematical concepts and real-world problem-solving. The detailed exploration of the factors of 57 serves as a stepping stone for understanding the broader principles of number theory and its applications.
Latest Posts
Latest Posts
-
Is 12 Prime Or Composite Number
Apr 07, 2025
-
1 4 Mile Is How Many Feet
Apr 07, 2025
-
Ratio Word Problems Worksheets With Answers
Apr 07, 2025
-
What Is The Square Root Of 4096
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Is A Factor Of 57 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
