What Is A Fraction Equivalent To 2 3
News Co
Apr 05, 2025 · 5 min read
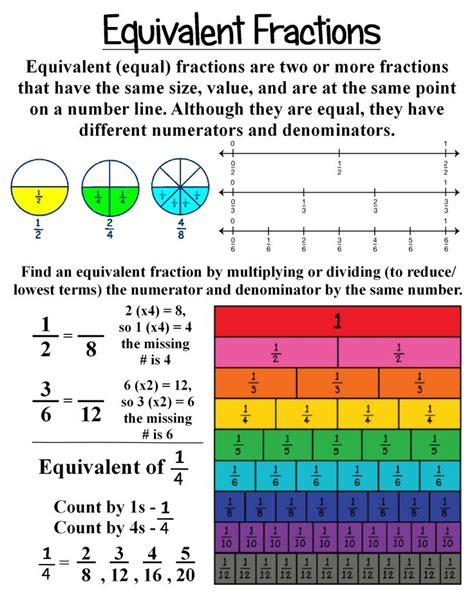
Table of Contents
What is a Fraction Equivalent to 2/3? Exploring Equivalent Fractions and Their Applications
Understanding fractions is fundamental to mathematics and numerous real-world applications. This comprehensive guide delves into the concept of equivalent fractions, specifically focusing on finding fractions equivalent to 2/3. We'll explore various methods for determining these equivalents, discuss their practical uses, and offer examples to solidify your understanding.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion of a whole, even though they appear different. Think of slicing a pizza: one-half (1/2) is the same as two-quarters (2/4), or four-eighths (4/8), all representing half the pizza. The key is that the ratio between the numerator (top number) and the denominator (bottom number) remains constant.
Key Concept: To find an equivalent fraction, you multiply or divide both the numerator and the denominator by the same non-zero number. This maintains the proportional relationship, ensuring the new fraction represents the same value.
Finding Fractions Equivalent to 2/3
Let's apply this principle to find fractions equivalent to 2/3. We can achieve this by multiplying both the numerator (2) and the denominator (3) by the same integer.
Multiplying to Find Equivalents
Let's find a few equivalent fractions by multiplying:
- Multiply by 2: (2 x 2) / (3 x 2) = 4/6
- Multiply by 3: (2 x 3) / (3 x 3) = 6/9
- Multiply by 4: (2 x 4) / (3 x 4) = 8/12
- Multiply by 5: (2 x 5) / (3 x 5) = 10/15
- Multiply by 10: (2 x 10) / (3 x 10) = 20/30
As you can see, we can generate an infinite number of equivalent fractions simply by multiplying the numerator and denominator by different integers. Each of these fractions—4/6, 6/9, 8/12, 10/15, 20/30, and countless others—represents exactly the same value as 2/3.
Simplifying Fractions (Finding Equivalent Fractions by Dividing)
The reverse process, simplifying a fraction, also reveals equivalent fractions. Simplifying involves dividing both the numerator and denominator by their greatest common divisor (GCD). For instance, let's consider the fraction 12/18.
The GCD of 12 and 18 is 6. Dividing both by 6 gives us:
(12 ÷ 6) / (18 ÷ 6) = 2/3
This demonstrates that 12/18 is an equivalent fraction to 2/3. Simplifying fractions is crucial for expressing them in their simplest form—a form where the numerator and denominator share no common factors other than 1.
Visualizing Equivalent Fractions
Understanding equivalent fractions is often easier with visual aids. Imagine a rectangular bar divided into three equal parts. Shading two of these parts represents 2/3. Now, imagine dividing each of those three parts in half. You now have six equal parts, and four of them are shaded (4/6), still representing the same portion of the bar as 2/3. This visual representation helps solidify the concept of equivalent fractions.
Applications of Equivalent Fractions in Real-World Scenarios
Equivalent fractions are not just an abstract mathematical concept; they have significant practical applications in various fields:
Cooking and Baking
Recipes often require adjusting ingredient quantities. If a recipe calls for 2/3 cup of flour, but you want to make a larger batch, you might need to find an equivalent fraction, such as 4/6 cup or 6/9 cup, depending on your desired scaling factor.
Measurement and Conversions
Converting between units of measurement often relies on equivalent fractions. For instance, converting inches to feet involves using equivalent fractions: 12 inches = 1 foot, so 24 inches would be represented as 24/12 = 2 feet.
Construction and Engineering
Precise measurements and scaling are critical in construction and engineering. Equivalent fractions allow for calculations and adjustments while ensuring proportions remain accurate.
Finance and Budgeting
Understanding fractions and their equivalents is essential for managing finances. Calculating percentages, understanding proportions of budgets, and determining loan interest rates all involve manipulating fractions and their equivalent forms.
Data Analysis and Statistics
Representing data and proportions in various forms often involves using equivalent fractions and simplifying them for clarity and easier interpretation.
Identifying Equivalent Fractions: A Step-by-Step Guide
To determine if two fractions are equivalent, follow these steps:
-
Cross-Multiplication: Multiply the numerator of the first fraction by the denominator of the second fraction. Then multiply the denominator of the first fraction by the numerator of the second fraction.
-
Comparison: If the products from step 1 are equal, the fractions are equivalent. If not, they are not equivalent.
Example: Are 2/3 and 6/9 equivalent?
- (2 x 9) = 18
- (3 x 6) = 18
Since the products are equal, 2/3 and 6/9 are equivalent fractions.
Advanced Concepts Related to Equivalent Fractions
While the basic principles are straightforward, understanding equivalent fractions can lead to more complex concepts:
-
Least Common Denominator (LCD): Finding the LCD is crucial when adding or subtracting fractions. The LCD is the smallest common denominator for a set of fractions.
-
Rational Numbers: Equivalent fractions are a subset of rational numbers, which are numbers that can be expressed as a fraction of two integers (where the denominator is not zero).
-
Decimal Representation: Every fraction has an equivalent decimal representation. For example, 2/3 is equivalent to the repeating decimal 0.666...
Conclusion: Mastering Equivalent Fractions
Mastering the concept of equivalent fractions is a cornerstone of mathematical proficiency. This involves understanding how to find equivalent fractions by multiplying or dividing both the numerator and denominator by the same number, simplifying fractions to their simplest form, and applying this knowledge to various real-world situations. From baking a cake to analyzing financial data, the ability to work with equivalent fractions proves invaluable in many aspects of life. The methods and examples provided in this guide should equip you with the skills and understanding necessary to confidently work with equivalent fractions. Regular practice and application will solidify your grasp of this important mathematical concept and its wide-ranging uses.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is A Fraction Equivalent To 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.