What Is A Half Of 1/2
News Co
Apr 24, 2025 · 4 min read
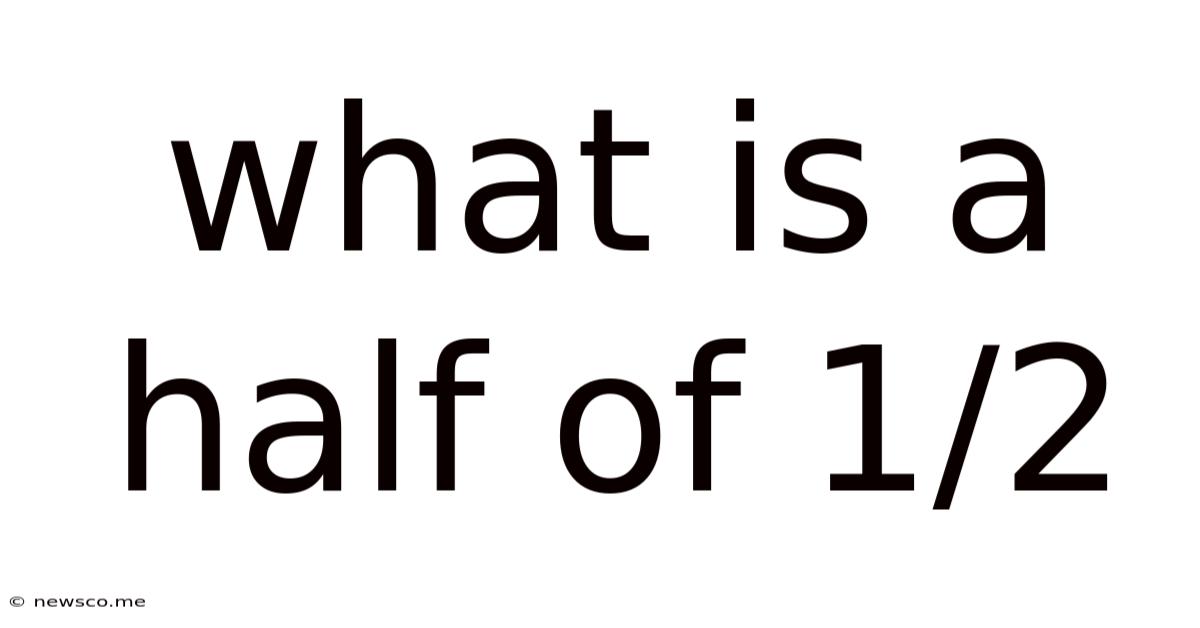
Table of Contents
What is Half of 1/2? A Deep Dive into Fractions and Division
This seemingly simple question, "What is half of 1/2?", opens the door to a fascinating exploration of fractions, division, and the fundamental principles of mathematics. While the answer itself is straightforward, understanding the underlying concepts allows for a much deeper appreciation of mathematical operations and their practical applications. This article will not only provide the answer but delve into the 'why' behind the solution, exploring various methods to arrive at the correct result and expanding upon related mathematical concepts.
Understanding Fractions: The Building Blocks
Before tackling the problem, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating how many equal parts the whole is divided into.
In our case, we're dealing with the fraction 1/2, which represents one out of two equal parts of a whole. Think of a pizza cut into two equal slices; 1/2 represents one of those slices.
Calculating Half of 1/2: The Core Problem
The question "What is half of 1/2?" can be rephrased mathematically as:
(1/2) / 2 or (1/2) x (1/2)
Both representations are valid and lead to the same solution. Let's explore each method:
Method 1: Division
Dividing a fraction by a whole number involves multiplying the fraction's denominator by the whole number. Therefore:
(1/2) / 2 = 1 / (2 x 2) = 1/4
This means that half of one-half is one-quarter.
Method 2: Multiplication
Multiplying fractions involves multiplying the numerators together and the denominators together. Therefore:
(1/2) x (1/2) = (1 x 1) / (2 x 2) = 1/4
This again confirms that half of one-half is one-quarter.
Visualizing the Solution: A Practical Approach
Visual aids can significantly enhance our understanding of fractions and their operations. Imagine a rectangle representing a whole.
- Divide the rectangle in half: This represents 1/2.
- Divide each half in half again: This further divides the rectangle into four equal parts.
- Highlight one of the four parts: This visually demonstrates that half of 1/2 is 1/4.
This simple visual representation solidifies the mathematical result and makes the concept more intuitive.
Expanding on Fraction Operations: Beyond the Basics
Understanding half of 1/2 is a stepping stone to more complex fraction operations. Let's explore some related concepts:
Adding and Subtracting Fractions
Adding and subtracting fractions requires a common denominator. For example:
1/2 + 1/4 = 2/4 + 1/4 = 3/4
This highlights the importance of understanding equivalent fractions.
Multiplying and Dividing Fractions
As demonstrated earlier, multiplying fractions involves multiplying the numerators and denominators separately. Dividing fractions is equivalent to multiplying by the reciprocal of the second fraction. For example:
1/2 ÷ 1/4 = 1/2 x 4/1 = 4/2 = 2
Simplifying Fractions
Fractions can often be simplified by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. For example:
4/8 = (4/4) / (8/4) = 1/2
Simplifying fractions is crucial for expressing them in their simplest form.
Real-World Applications of Fractions and Division
The ability to understand and manipulate fractions is not confined to the classroom; it's vital in numerous real-world scenarios:
- Cooking and Baking: Recipes often require precise measurements, involving fractions of cups, teaspoons, and tablespoons.
- Construction and Engineering: Accurate calculations involving fractions are crucial for designing and building structures.
- Finance and Budgeting: Managing finances involves understanding fractions and percentages for budgeting, investments, and loans.
- Data Analysis: Representing and interpreting data often involves working with fractions and proportions.
Advanced Concepts: Extending the Knowledge
For those seeking a deeper understanding, let's explore some advanced concepts related to fractions:
Decimal Representation of Fractions
Fractions can be converted into decimals by dividing the numerator by the denominator. For example:
1/4 = 0.25
Percentage Representation of Fractions
Fractions can also be expressed as percentages by multiplying the fraction by 100%. For example:
1/4 = (1/4) x 100% = 25%
Working with Mixed Numbers
Mixed numbers combine a whole number and a fraction. For example, 1 1/2 represents one and a half. Operations involving mixed numbers require converting them to improper fractions before performing calculations.
Conclusion: Mastering the Fundamentals
The seemingly simple question, "What is half of 1/2?", serves as a powerful gateway to understanding fundamental mathematical concepts. Mastering fraction operations, including addition, subtraction, multiplication, and division, is not merely an academic exercise; it's a practical skill applicable to countless aspects of daily life. By thoroughly grasping these concepts, we build a solid foundation for more advanced mathematical pursuits and develop the problem-solving skills essential for navigating a complex world. Remember, the beauty of mathematics lies not just in the answers but in the journey of understanding the underlying principles and their far-reaching applications. Continue to explore, question, and expand your mathematical horizons – the possibilities are limitless.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is A Half Of 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.