What Is A Prime Factorization Of 44
News Co
Apr 05, 2025 · 5 min read
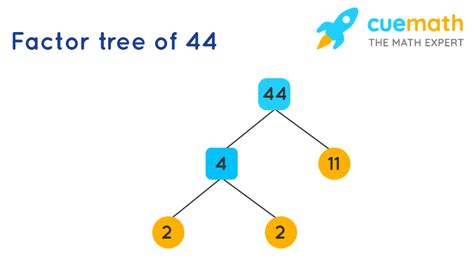
Table of Contents
What is the Prime Factorization of 44? A Deep Dive into Prime Numbers and Factorization
Prime factorization. The term itself might sound intimidating, conjuring up images of complex mathematical equations and endless calculations. But at its core, prime factorization is a fundamental concept in number theory, offering a simple yet powerful way to understand the building blocks of whole numbers. This article will explore the prime factorization of 44, providing a comprehensive understanding of the process and its significance within mathematics. We'll delve into the definitions of prime numbers and factors, walk through the factorization process step-by-step, and then discuss the broader applications and implications of prime factorization.
Understanding Prime Numbers and Factors
Before embarking on the prime factorization of 44, let's solidify our understanding of the key terms:
What are Prime Numbers?
A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This means it's not divisible by any other whole number without leaving a remainder. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. Prime numbers are the fundamental building blocks of all other whole numbers. They are indivisible and cannot be broken down further into smaller whole number factors.
What are Factors?
Factors are whole numbers that divide evenly into another whole number without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides perfectly into 12. Finding all the factors of a number is a crucial step in determining its prime factorization.
The Prime Factorization of 44: A Step-by-Step Approach
Now, let's tackle the prime factorization of 44. The goal is to express 44 as a product of only prime numbers. We can achieve this using a method called the factor tree.
Step 1: Find any two factors of 44.
The most obvious starting point is to recognize that 44 is an even number, meaning it's divisible by 2. Therefore, we can write:
44 = 2 x 22
Step 2: Continue factoring until all factors are prime.
We've broken down 44 into 2 and 22. Notice that 2 is a prime number. However, 22 is not prime; it's divisible by 2. So we continue factoring 22:
22 = 2 x 11
Step 3: Express 44 as a product of prime factors.
Now we have factored 44 completely into prime numbers: 2, 2, and 11. Therefore, the prime factorization of 44 is:
44 = 2 x 2 x 11 or 2² x 11
This representation shows that 44 is composed entirely of the prime numbers 2 and 11. No matter how you try to factor 44, you'll always end up with these same prime numbers.
Alternative Methods for Prime Factorization
While the factor tree method is visually intuitive, other methods can also be used to find the prime factorization of a number. One such method involves systematically dividing the number by prime numbers, starting with the smallest prime number (2) and working your way up.
Let's apply this method to 44:
- Divide by 2: 44 / 2 = 22
- Divide by 2 again: 22 / 2 = 11
- 11 is a prime number, so we stop here.
This method yields the same result: 2 x 2 x 11, or 2² x 11.
The Significance of Prime Factorization
The prime factorization of a number might seem like a simple mathematical exercise, but it has profound implications across various fields:
1. Cryptography
Prime factorization plays a crucial role in modern cryptography, particularly in public-key cryptography systems like RSA. These systems rely on the difficulty of factoring extremely large numbers into their prime factors. The security of these systems depends on the computational infeasibility of factoring such numbers, even with powerful computers.
2. Number Theory
Prime factorization is a cornerstone of number theory, a branch of mathematics that explores the properties of whole numbers. It's used to prove many important theorems and solve complex mathematical problems.
3. Simplifying Fractions
Prime factorization is essential for simplifying fractions to their lowest terms. By finding the prime factors of both the numerator and the denominator, we can cancel out common factors and reduce the fraction.
4. Finding the Least Common Multiple (LCM) and Greatest Common Divisor (GCD)
Prime factorization provides an efficient method for finding the LCM and GCD of two or more numbers. The LCM is the smallest number that is a multiple of all the given numbers, while the GCD is the largest number that divides all the given numbers without leaving a remainder.
5. Abstract Algebra
Prime factorization has applications in abstract algebra, a field that studies algebraic structures like groups, rings, and fields. The unique factorization theorem, which states that every integer greater than 1 can be uniquely expressed as a product of prime numbers, is a fundamental result in abstract algebra.
Beyond 44: Exploring Other Prime Factorizations
Let's briefly explore the prime factorizations of some related numbers to further solidify our understanding:
- 45: 3² x 5
- 46: 2 x 23
- 48: 2⁴ x 3
- 49: 7²
- 50: 2 x 5²
Notice how each number can be uniquely expressed as a product of prime factors. This uniqueness is a fundamental property of prime factorization.
Conclusion: The Enduring Importance of Prime Factorization
The prime factorization of 44 – 2² x 11 – might appear to be a straightforward calculation. However, the underlying concepts and applications extend far beyond this simple example. From securing online transactions to unlocking deeper mathematical truths, prime factorization remains a fundamental and crucial concept in mathematics and computer science. Understanding the process and its implications offers a valuable insight into the structure and beauty of numbers. This seemingly simple concept forms the bedrock of many complex mathematical processes and plays a crucial role in modern technology. So, the next time you encounter a number, remember the power and elegance hidden within its prime factorization.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is A Prime Factorization Of 44 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.