What Is An Equation Of A Horizontal Line
News Co
Apr 06, 2025 · 5 min read
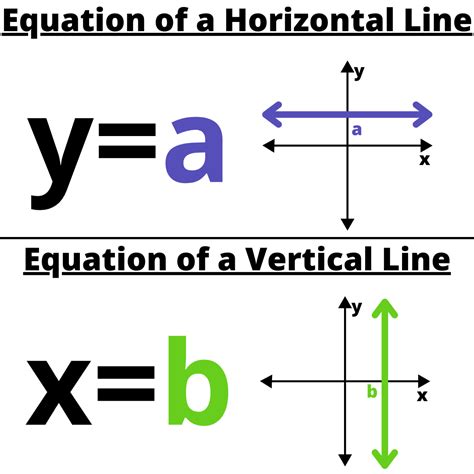
Table of Contents
What is the Equation of a Horizontal Line? A Comprehensive Guide
Understanding the equation of a horizontal line is fundamental to grasping core concepts in algebra and coordinate geometry. This comprehensive guide will delve into the topic, exploring its definition, derivation, real-world applications, and related concepts. We'll also tackle common misconceptions and provide plenty of examples to solidify your understanding.
Defining a Horizontal Line
A horizontal line is a straight line that runs parallel to the x-axis on a Cartesian coordinate plane. It possesses a constant y-value for all points along its length. This means no matter what the x-coordinate is, the y-coordinate remains unchanged. This consistent y-value is the key to understanding its equation.
Visualizing a Horizontal Line
Imagine a perfectly level road stretching out before you. That's a perfect representation of a horizontal line. No matter how far you walk along the road (changing your x-coordinate), your height above sea level (y-coordinate) remains constant.
Deriving the Equation: Why y = c?
The equation of a horizontal line is always in the form y = c, where 'c' is a constant representing the y-intercept. Let's break down why:
-
The Slope: The slope of a line indicates its steepness. A horizontal line has zero slope. This is because there's no change in the y-value, regardless of the change in the x-value. Remember the slope formula: m = (y₂ - y₁) / (x₂ - x₁). If y₂ = y₁, then the numerator becomes zero, resulting in a slope of zero.
-
The y-intercept: The y-intercept is the point where the line intersects the y-axis. This is where x = 0. Since the y-value remains constant along the entire line, the y-intercept is simply the constant value 'c'.
-
Point-Slope Form: We can also derive the equation from the point-slope form of a line: y - y₁ = m(x - x₁). Since the slope (m) is 0, the equation simplifies to y - y₁ = 0, which further simplifies to y = y₁. Replacing y₁ with the constant 'c', we get the familiar equation y = c.
Examples of Horizontal Line Equations
Let's illustrate with some examples:
-
y = 5: This represents a horizontal line passing through all points where the y-coordinate is 5, regardless of the x-coordinate. Points like (1, 5), (-3, 5), (0, 5), and (100, 5) all lie on this line.
-
y = -2: This represents a horizontal line passing through all points where the y-coordinate is -2.
-
y = 0: This is a special case – it represents the x-axis itself. The x-axis is a horizontal line where the y-coordinate is always 0.
Distinguishing Horizontal Lines from Vertical Lines
It's crucial to differentiate between horizontal and vertical lines. While a horizontal line has an equation of the form y = c, a vertical line has an equation of the form x = k, where 'k' is a constant representing the x-intercept. A vertical line has an undefined slope because the denominator in the slope formula becomes zero (Δx = 0).
Real-World Applications of Horizontal Lines
Horizontal lines appear frequently in various real-world scenarios:
-
Mapping and Geography: Contour lines on topographic maps often represent lines of constant elevation, which are horizontal lines. Similarly, lines of latitude are horizontal lines on a globe.
-
Engineering and Construction: Horizontal lines are crucial in blueprints and architectural designs, representing level surfaces and structures. They guide construction and ensure accuracy.
-
Data Representation: In data visualization, horizontal lines can represent constant values or thresholds in graphs and charts.
-
Physics: In physics, horizontal lines can illustrate constant velocity or displacement in certain scenarios.
Solving Problems Involving Horizontal Lines
Let's examine some problem types:
Problem 1: Finding the equation of a horizontal line passing through a given point.
Question: Find the equation of the horizontal line passing through the point (4, -7).
Solution: Since it's a horizontal line, the y-coordinate remains constant. Therefore, the equation is simply y = -7.
Problem 2: Determining if a point lies on a horizontal line.
Question: Does the point (2, 3) lie on the horizontal line y = 5?
Solution: No. The y-coordinate of the point (2, 3) is 3, which is different from the constant y-value (5) of the line y = 5.
Problem 3: Finding the intersection of a horizontal line and another line.
Question: Find the intersection point of the horizontal line y = 2 and the line y = x + 1.
Solution: Substitute y = 2 into the equation y = x + 1: 2 = x + 1. Solving for x, we get x = 1. The intersection point is (1, 2).
Common Misconceptions and Clarifications
-
Confusing slope with the equation: While the slope of a horizontal line is 0, the equation is not y = 0 unless the line is specifically the x-axis.
-
Assuming all horizontal lines are the same: Horizontal lines are parallel to each other but not identical. Each horizontal line has a unique constant y-value.
-
Neglecting the significance of the constant 'c': The constant 'c' represents a specific y-coordinate, defining the exact position of the horizontal line.
Advanced Concepts and Extensions
-
Parallel Lines: All horizontal lines are parallel to each other because they all have a slope of 0.
-
Perpendicular Lines: A horizontal line is perpendicular to any vertical line.
-
Systems of Equations: Solving systems of equations involving horizontal lines often simplifies the process.
-
Functions: A horizontal line can represent a constant function, where the output (y-value) is always the same, regardless of the input (x-value).
Conclusion: Mastering Horizontal Lines
Understanding the equation of a horizontal line (y = c) is a cornerstone of fundamental algebra and geometry. Its simplicity belies its importance in various applications. By mastering this concept, you’ll build a strong foundation for more advanced mathematical concepts and problem-solving. Remember to practice solving various problems, visualize the lines on a coordinate plane, and differentiate it from vertical lines to ensure complete understanding. This comprehensive guide has equipped you with the knowledge and tools to confidently tackle any problem involving horizontal lines.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is An Equation Of A Horizontal Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.