What Is An Equivalent Fraction For 2/3
News Co
Apr 05, 2025 · 5 min read
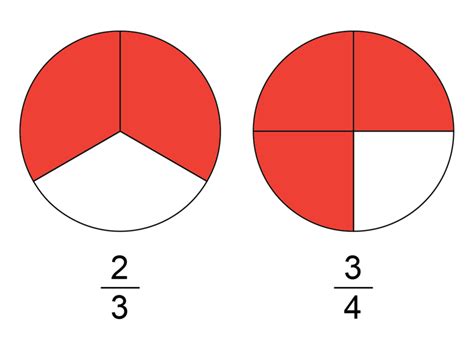
Table of Contents
What is an Equivalent Fraction for 2/3? A Deep Dive into Fraction Equivalence
Understanding equivalent fractions is a fundamental concept in mathematics, crucial for mastering various arithmetic operations and problem-solving skills. This article delves deep into the concept of equivalent fractions, focusing specifically on finding equivalent fractions for 2/3. We'll explore different methods, provide numerous examples, and highlight the importance of this concept in real-world applications.
Understanding Fractions and Equivalence
Before diving into finding equivalent fractions for 2/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator represents the number of parts being considered.
Equivalent fractions are fractions that represent the same value, even though they look different. They represent the same portion of a whole. For example, 1/2 and 2/4 are equivalent fractions because they both represent one-half of a whole.
Methods for Finding Equivalent Fractions for 2/3
There are several ways to find equivalent fractions for 2/3:
1. Multiplying the Numerator and Denominator by the Same Number
The most common and straightforward method is to multiply both the numerator and the denominator of the fraction by the same non-zero number. This is based on the fundamental principle that multiplying a number by 1 doesn't change its value. Since multiplying the numerator and denominator by the same number is the same as multiplying the fraction by 1 (e.g., 3/3 = 1), the value of the fraction remains unchanged.
Let's illustrate this with 2/3:
- Multiplying by 2: (2 x 2) / (3 x 2) = 4/6
- Multiplying by 3: (2 x 3) / (3 x 3) = 6/9
- Multiplying by 4: (2 x 4) / (3 x 4) = 8/12
- Multiplying by 5: (2 x 5) / (3 x 5) = 10/15
Therefore, 4/6, 6/9, 8/12, 10/15, and infinitely many other fractions are equivalent to 2/3. You can continue this process indefinitely by multiplying by any non-zero whole number.
2. Dividing the Numerator and Denominator by the Same Number (Simplification)
The reverse process is also true. If you can find a common factor (a number that divides both the numerator and the denominator without leaving a remainder) for both the numerator and the denominator, you can divide both by that factor to simplify the fraction. This process yields an equivalent fraction, but in a simpler form.
While 2/3 is already in its simplest form (no common factors other than 1), let's consider an equivalent fraction like 6/9. Both 6 and 9 are divisible by 3:
6 ÷ 3 = 2 9 ÷ 3 = 3
Therefore, 6/9 simplifies to 2/3. This demonstrates that simplification leads to an equivalent fraction in its simplest form.
3. Using Visual Representations
Visual aids, such as diagrams and models, can effectively demonstrate the concept of equivalent fractions. Imagine a circle divided into three equal parts, with two parts shaded. This visually represents 2/3. Now, imagine dividing each of those three parts into two equal parts. You now have six parts, and four of them are shaded. This visually represents 4/6, clearly showing its equivalence to 2/3.
Why is Understanding Equivalent Fractions Important?
The ability to identify and work with equivalent fractions is essential for several mathematical operations and real-world applications:
-
Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. Finding equivalent fractions with a common denominator is crucial for performing these operations accurately. For example, adding 2/3 and 1/6 requires finding an equivalent fraction for 2/3 with a denominator of 6 (which is 4/6).
-
Comparing Fractions: Determining which of two fractions is larger or smaller often involves finding equivalent fractions with a common denominator to facilitate direct comparison.
-
Simplifying Fractions: Simplifying fractions to their simplest form makes them easier to understand and work with. This involves finding equivalent fractions with the smallest possible numerator and denominator.
-
Ratio and Proportion Problems: Equivalent fractions are fundamental in solving ratio and proportion problems, which are common in many fields, including cooking, construction, and science.
-
Decimal Conversion: Converting fractions to decimals and vice versa often involves finding equivalent fractions with denominators that are powers of 10 (e.g., 10, 100, 1000), making the conversion straightforward.
Real-World Applications of Equivalent Fractions
The practical applications of equivalent fractions extend beyond the classroom:
-
Cooking: Recipe scaling often requires working with equivalent fractions. If a recipe calls for 2/3 cup of flour, and you want to double the recipe, you need to understand that 2/3 doubled is equivalent to 4/3 or 1 and 1/3 cups.
-
Construction: Measurements in construction projects frequently involve fractions. Converting measurements from one unit to another might require using equivalent fractions.
-
Sewing: Pattern making and fabric cutting involve working with fractional measurements. Understanding equivalent fractions ensures accurate cutting and sewing.
-
Data Analysis: Representing data visually using pie charts or bar graphs often involves working with fractions and percentages, which are closely related to the concept of equivalent fractions.
Advanced Concepts Related to Equivalent Fractions
While we've primarily focused on the basic principles, the concept of equivalent fractions extends to more advanced mathematical areas:
-
Rational Numbers: Equivalent fractions are a cornerstone of understanding rational numbers – numbers that can be expressed as a ratio of two integers.
-
Algebra: Manipulating algebraic expressions often involves simplifying fractions, requiring a deep understanding of equivalent fractions.
-
Calculus: Concepts related to limits and continuity build upon the foundation of understanding equivalent fractions and their properties.
Conclusion: Mastering Equivalent Fractions
Understanding equivalent fractions is a crucial stepping stone in mastering various mathematical concepts and problem-solving skills. By mastering the techniques of finding and working with equivalent fractions, you'll build a strong foundation for future mathematical learning and effectively apply these skills to real-world situations. The seemingly simple concept of equivalent fractions for 2/3, as demonstrated throughout this article, unlocks a deeper understanding of fractions and their crucial role in mathematics and beyond. Remember to practice regularly, using different methods and real-world examples, to solidify your understanding.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is An Equivalent Fraction For 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.