What Is Half Of 1 1/4
News Co
Mar 24, 2025 · 5 min read
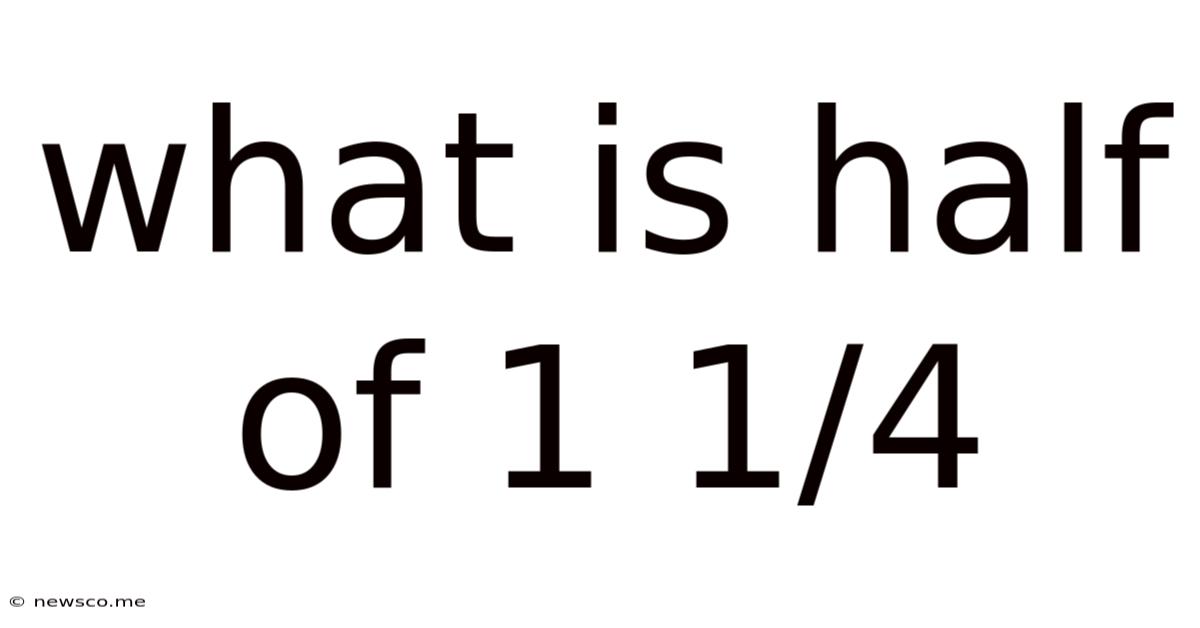
Table of Contents
What is Half of 1 ¼? A Deep Dive into Fractions and Their Applications
This seemingly simple question, "What is half of 1 ¼?", opens a door to a fascinating world of fractions, mathematical operations, and their practical applications in everyday life. While the answer itself is straightforward, understanding the underlying concepts provides a strong foundation for more complex mathematical problems. This article will not only solve the problem but also explore the various methods for solving it, discuss the importance of understanding fractions, and delve into real-world examples where such calculations are crucial.
Understanding Fractions: A Foundation for Success
Before we dive into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
In our problem, 1 ¼ is a mixed number. A mixed number combines a whole number (1 in this case) and a proper fraction (¼). To work with this effectively, it's often helpful to convert it into an improper fraction.
Converting Mixed Numbers to Improper Fractions
To convert 1 ¼ to an improper fraction, we multiply the whole number (1) by the denominator (4) and then add the numerator (1). This result becomes the new numerator, while the denominator remains the same.
1 ¼ = (1 x 4 + 1) / 4 = 5/4
Now we have an improper fraction where the numerator (5) is larger than the denominator (4). This representation makes the calculation much easier.
Calculating Half of 1 ¼: Multiple Approaches
Now that we've converted 1 ¼ to 5/4, we can proceed to find half of it. There are several ways to do this:
Method 1: Direct Multiplication
The most straightforward method involves multiplying 5/4 by ½:
(5/4) x (½) = (5 x 1) / (4 x 2) = 5/8
Therefore, half of 1 ¼ is 5/8.
Method 2: Dividing by 2
Alternatively, we can divide the improper fraction 5/4 by 2. Remember that dividing by 2 is the same as multiplying by ½:
(5/4) ÷ 2 = (5/4) x (½) = 5/8
This again confirms that half of 1 ¼ is 5/8.
Method 3: Working with the Mixed Number Directly (Less Efficient)
While less efficient, we can also work directly with the mixed number 1 ¼. We can find half of the whole number (1) and half of the fraction (¼) separately:
- Half of 1 is ½
- Half of ¼ is (¼) x (½) = ⅛
Adding these together, we get: ½ + ⅛ = ⁴/₈ + ⅛ = ⁵/₈
This method demonstrates that even when working with mixed numbers directly, we arrive at the same answer: 5/8.
The Significance of Understanding Fractions
The ability to manipulate and understand fractions is fundamental to many areas of life, not just mathematics. Here are some examples where a solid grasp of fractions is essential:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Understanding fractions ensures you accurately measure and achieve the desired results. Imagine trying to bake a cake without knowing how much ½ cup or ⅓ cup means!
-
Construction and Engineering: Precise measurements are critical in construction and engineering. Fractions are frequently used in blueprints and design specifications to ensure accuracy and structural integrity.
-
Finance and Budgeting: Understanding fractions is crucial for managing personal finances. Calculating percentages, interest rates, and proportions all rely on the principles of fractions.
-
Data Analysis and Statistics: Fractions and percentages are essential for representing data and drawing conclusions. Understanding ratios and proportions is central to data interpretation and statistical analysis.
-
Everyday Problem Solving: Many everyday situations involve dividing quantities or sharing resources, which necessitates the use of fractions. For example, sharing a pizza among friends, dividing a workload, or calculating discounts all involve fractional concepts.
Beyond the Basics: Extending Fractional Concepts
While we've addressed the core question, understanding fractions extends beyond simple calculations. Let's explore some related concepts:
Decimal Representation
Fractions can be easily converted to decimals by dividing the numerator by the denominator. In our case:
5/8 = 0.625
This decimal representation provides another way to represent the answer.
Percentage Representation
Decimals can be converted to percentages by multiplying by 100. Thus, 0.625 becomes 62.5%. This means half of 1 ¼ is 62.5% of the original quantity.
Equivalent Fractions
It's important to understand that multiple fractions can represent the same value. For example, 5/8 is equivalent to 10/16, 15/24, and many other fractions. The ability to identify equivalent fractions is important for simplifying calculations and comparing values.
Practical Applications and Real-World Scenarios
The concept of finding half of a quantity is deeply ingrained in our everyday lives. Here are a few examples:
-
Sharing Resources: If you have 1 ¼ pizzas and want to share them equally among two people, each person receives 5/8 of a pizza.
-
Cutting Materials: If you have 1 ¼ meters of fabric and need to cut it in half, you'll have two pieces, each measuring 5/8 meters long.
-
Dividing Tasks: If a task takes 1 ¼ hours to complete, and you want to divide the workload equally between two people, each person will spend 5/8 of an hour on the task.
Conclusion: Mastering Fractions for a Brighter Future
The question "What is half of 1 ¼?" seems simple at first glance, but its solution reveals the richness and importance of understanding fractions. By mastering the concepts discussed here—converting mixed numbers, multiplying and dividing fractions, understanding decimal and percentage equivalents, and recognizing equivalent fractions—you will significantly enhance your mathematical abilities and equip yourself to solve a wide array of real-world problems. Fractions are not just abstract mathematical concepts; they are fundamental tools for navigating the complexities of our everyday lives. The more you understand them, the more proficient you'll become at problem-solving and critical thinking in numerous contexts. Remember, a solid foundation in fractions is a cornerstone of mathematical literacy and a valuable asset in many fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is Half Of 1 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.