What Is Half Of 1 1 8
News Co
Apr 02, 2025 · 5 min read
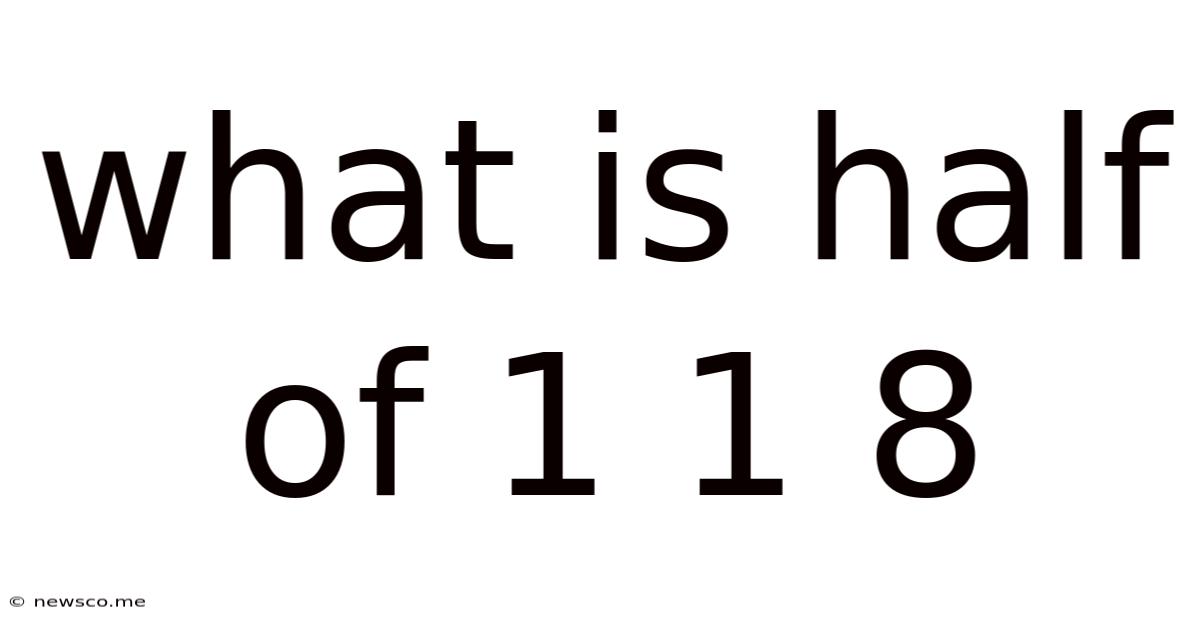
Table of Contents
What is Half of 1 1/8? A Deep Dive into Fractions and Their Applications
The seemingly simple question, "What is half of 1 1/8?" opens a door to a fascinating world of mathematical concepts, practical applications, and problem-solving strategies. While the answer itself is straightforward, understanding the process behind arriving at that answer lays the groundwork for more complex mathematical endeavors. This article will explore not only the solution but also the underlying principles of fractions, mixed numbers, and their relevance in various real-world scenarios.
Understanding the Basics: Fractions and Mixed Numbers
Before diving into the calculation, let's solidify our understanding of the fundamental components: fractions and mixed numbers.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For instance, 1/2 represents one out of two equal parts, while 3/4 represents three out of four equal parts.
Mixed Numbers: A mixed number combines a whole number and a fraction. For example, 1 1/8 means one whole unit plus one-eighth of another unit. This representation is often more intuitive than using improper fractions (where the numerator is larger than the denominator) for representing quantities greater than one. Converting between mixed numbers and improper fractions is a crucial skill in working with fractions.
Converting Mixed Numbers to Improper Fractions
To easily calculate half of 1 1/8, converting the mixed number into an improper fraction is highly beneficial. The process is as follows:
- Multiply the whole number by the denominator: 1 * 8 = 8
- Add the numerator: 8 + 1 = 9
- Keep the same denominator: The denominator remains 8.
Therefore, 1 1/8 is equivalent to the improper fraction 9/8.
Calculating Half: Division by Two
Now that we have 1 1/8 expressed as the improper fraction 9/8, finding half is simply a matter of dividing by 2. We can do this by multiplying the fraction by 1/2:
(9/8) * (1/2) = 9/16
Therefore, half of 1 1/8 is 9/16.
Converting Back to a Mixed Number (Optional)
While 9/16 is a perfectly acceptable answer, you might prefer expressing it as a mixed number for better comprehension. To do this:
- Divide the numerator by the denominator: 9 ÷ 16 = 0 with a remainder of 9.
- The quotient becomes the whole number: 0
- The remainder becomes the numerator, and the denominator stays the same: 9/16
Therefore, 9/16 can also be expressed as 0 9/16. Since the whole number is 0, it's usually written simply as 9/16.
Real-World Applications: Where Fractions Matter
Understanding fractions and mixed numbers isn't just about academic exercises; they are essential tools in numerous real-world situations:
-
Cooking and Baking: Recipes frequently involve fractional measurements of ingredients (e.g., 1 1/2 cups of flour, 1/4 teaspoon of salt). Accurate fractional calculations are crucial for successful cooking and baking.
-
Construction and Engineering: Precise measurements are paramount in these fields. Fractions are used in blueprints, calculations of material quantities, and ensuring structural integrity. Imagine calculating the length of a beam that needs to be cut into specific fractional lengths.
-
Finance and Budgeting: Dealing with percentages, interest rates, and dividing financial resources often involves fractional calculations. Understanding fractions is key to managing personal finances and making informed financial decisions.
-
Data Analysis and Statistics: Fractions and ratios are fundamental to expressing probabilities, proportions, and analyzing statistical data. Many statistical concepts rely on the precise manipulation of fractions.
-
Sewing and Tailoring: Accurate measurements are critical in garment construction. Fractional measurements are used extensively in pattern making and adjusting garment sizes.
-
Gardening and Landscaping: Calculating the amounts of fertilizer, seeds, or soil often requires working with fractions to ensure appropriate proportions.
-
Time Management: Dividing your time effectively often involves working with fractions of an hour or day. Scheduling and project management frequently utilize fractional time calculations.
Advanced Applications: Expanding the Concept
The ability to calculate half of 1 1/8 sets the stage for tackling more complex problems involving fractions. These include:
-
Adding and Subtracting Fractions: Mastering fraction addition and subtraction requires a deep understanding of common denominators and equivalent fractions.
-
Multiplying and Dividing Fractions: These operations involve multiplying numerators and denominators separately or inverting the second fraction for division.
-
Solving Equations with Fractions: This involves utilizing algebraic techniques to isolate and solve for unknown variables expressed in fractional form.
-
Working with Decimal Equivalents: Converting fractions to decimals and vice-versa allows for broader calculations and greater flexibility in problem-solving.
Problem-Solving Strategies: Approaching Fraction Problems Effectively
To confidently solve any problem involving fractions, employ these strategies:
-
Visualize the Problem: Imagine the fraction using a visual representation (e.g., a pie chart) to build intuition and understanding.
-
Simplify Fractions: Reduce fractions to their simplest forms by finding common factors in the numerator and denominator.
-
Find Common Denominators: When adding or subtracting fractions with different denominators, find the least common multiple (LCM) to create equivalent fractions with a common denominator.
-
Break Down Complex Problems: Divide larger problems into smaller, more manageable steps.
-
Check Your Work: Always verify your answer using alternative methods or estimation to ensure accuracy.
Conclusion: The Power of Fractional Understanding
The seemingly simple question of finding half of 1 1/8 opens a gateway to a comprehensive understanding of fractions, their applications, and their importance in various fields. Mastering fractional calculations empowers you to approach diverse real-world challenges with confidence and precision. By understanding the underlying principles and employing effective problem-solving strategies, you'll not only find the correct answer but also develop a crucial mathematical skillset that extends far beyond the realm of simple fractions. The ability to confidently work with fractions is a valuable asset in many aspects of life, making it a worthwhile investment of your time and effort. So, next time you encounter a problem involving fractions, remember the journey from 1 1/8 to 9/16, and the broader mathematical landscape it represents.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is Half Of 1 1 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.