What Is Half Of 1 3/8
News Co
May 03, 2025 · 4 min read
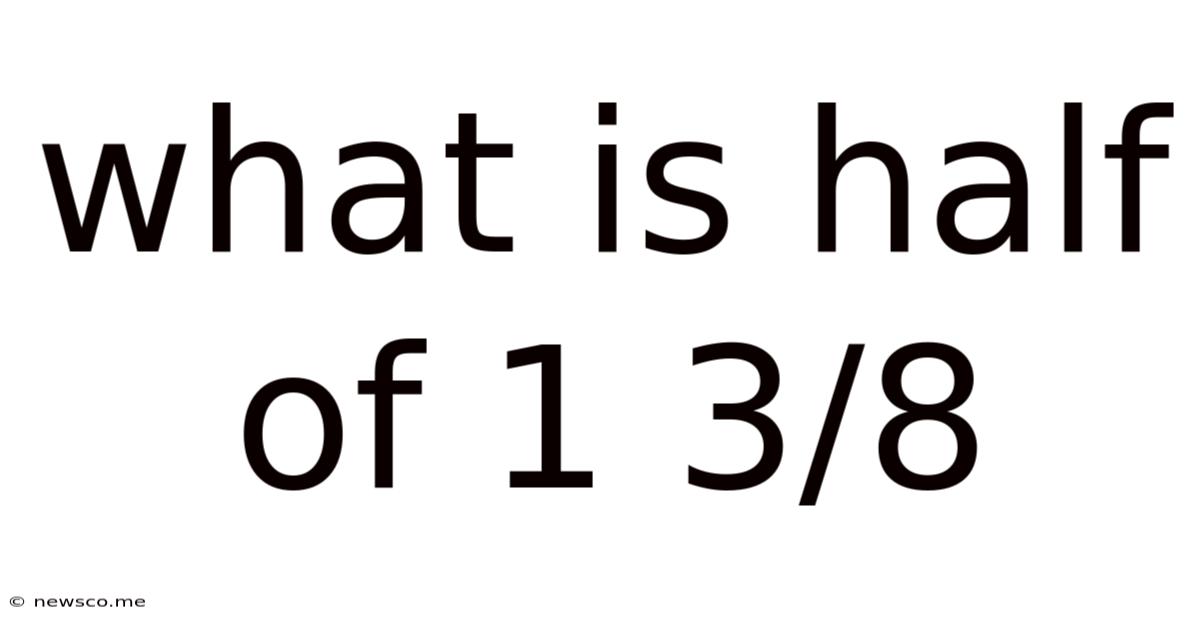
Table of Contents
What is Half of 1 3/8? A Comprehensive Guide to Fraction Division
Finding half of a mixed number like 1 3/8 might seem daunting at first, but with a clear understanding of fractions and a systematic approach, it becomes a straightforward calculation. This comprehensive guide will not only show you how to solve this specific problem but also equip you with the knowledge to tackle similar fraction division problems with confidence. We'll explore various methods, delve into the underlying principles, and even look at real-world applications where this type of calculation might be useful.
Understanding Mixed Numbers and Fractions
Before diving into the calculation, let's refresh our understanding of mixed numbers and fractions.
-
Mixed Numbers: A mixed number combines a whole number and a fraction, like 1 3/8. This represents one whole unit and three-eighths of another.
-
Improper Fractions: An improper fraction has a numerator (top number) larger than or equal to its denominator (bottom number). It represents a value greater than or equal to one. For example, 11/8 is an improper fraction equivalent to 1 3/8.
-
Proper Fractions: A proper fraction has a numerator smaller than its denominator, representing a value less than one (e.g., 3/8).
Method 1: Converting to an Improper Fraction
This is arguably the most common and efficient method for dividing mixed numbers. The process involves:
-
Converting the Mixed Number to an Improper Fraction: To convert 1 3/8 to an improper fraction, we multiply the whole number (1) by the denominator (8), add the numerator (3), and keep the same denominator: (1 * 8) + 3 = 11. Therefore, 1 3/8 becomes 11/8.
-
Dividing by 2 (or Multiplying by 1/2): Finding half of a number is equivalent to dividing by 2 or multiplying by its reciprocal, 1/2. So, we multiply 11/8 by 1/2:
(11/8) * (1/2) = 11/16
Therefore, half of 1 3/8 is 11/16.
Method 2: Dividing the Whole Number and Fraction Separately
This method offers a more intuitive approach, breaking down the problem into smaller, manageable steps:
-
Halving the Whole Number: Half of 1 is 1/2 or 0.5.
-
Halving the Fraction: Half of 3/8 is (3/8) / 2, which is equivalent to (3/8) * (1/2) = 3/16.
-
Combining the Results: Add the results from steps 1 and 2: 1/2 + 3/16. To add these fractions, we need a common denominator, which is 16. So we convert 1/2 to 8/16:
8/16 + 3/16 = 11/16
Again, half of 1 3/8 is 11/16.
Method 3: Decimal Conversion
While not always preferred for maintaining accuracy, particularly with complex fractions, converting to decimals can offer a quick approximation:
-
Convert the Mixed Number to a Decimal: 1 3/8 is equal to 1 + (3/8) = 1 + 0.375 = 1.375.
-
Divide by 2: 1.375 / 2 = 0.6875
-
Convert Back to a Fraction (Optional): 0.6875 can be converted back to a fraction. The process is to express the decimal as a fraction with a denominator of a power of 10 (e.g., 10, 100, 1000). 0.6875 = 6875/10000. Then simplify by finding the greatest common divisor (GCD) of 6875 and 10000, which is 625. Dividing both numerator and denominator by 625 gives us 11/16.
This confirms that half of 1 3/8 is 11/16.
Real-World Applications
Understanding fraction division, like finding half of 1 3/8, has numerous real-world applications:
-
Cooking and Baking: Recipes often require precise measurements. If a recipe calls for 1 3/8 cups of flour, and you want to halve the recipe, you'll need to know that half is 11/16 cups.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Calculating half of a dimension represented as a mixed number is a common task.
-
Sewing and Tailoring: Patterns and measurements in sewing often involve fractions and mixed numbers. Dividing measurements in half is frequently necessary.
-
Finance and Budgeting: When dealing with budgets or financial planning, understanding fraction division allows for accurate splitting of expenses or resources.
-
Data Analysis: Many datasets involve fractional values. Understanding how to manipulate and divide these values is essential for accurate data interpretation.
Further Practice and Exploration
To reinforce your understanding of fraction division, try solving similar problems:
- What is half of 2 1/4?
- What is one-third of 3 5/6?
- What is a quarter of 4 7/8?
By practicing these problems, you'll build confidence and fluency in working with fractions and mixed numbers. Remember to choose the method you find most comfortable and efficient.
Conclusion
Finding half of 1 3/8, or any mixed number, is a fundamental skill applicable in various fields. By understanding the different methods – converting to improper fractions, dividing the whole number and fraction separately, or using decimal conversions – you can approach these problems with confidence and accuracy. Mastering this skill lays a solid foundation for more advanced mathematical operations involving fractions and mixed numbers. Remember to always check your work and consider the context of the problem to determine the most suitable method for solving it. The ability to perform these calculations efficiently and accurately is invaluable in many aspects of life, from daily tasks to professional endeavors.
Latest Posts
Latest Posts
-
2 3 Cup Of Milk In Ml
May 03, 2025
-
Which Expression Is Equivalent To 6 8
May 03, 2025
-
Area Of A Triangle Inside A Circle
May 03, 2025
-
Find The Prime Factorization Of 40
May 03, 2025
-
Finding The Measure Of An Angle Worksheet
May 03, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 1 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.