What Is Half Of 5 5/8
News Co
Apr 23, 2025 · 4 min read
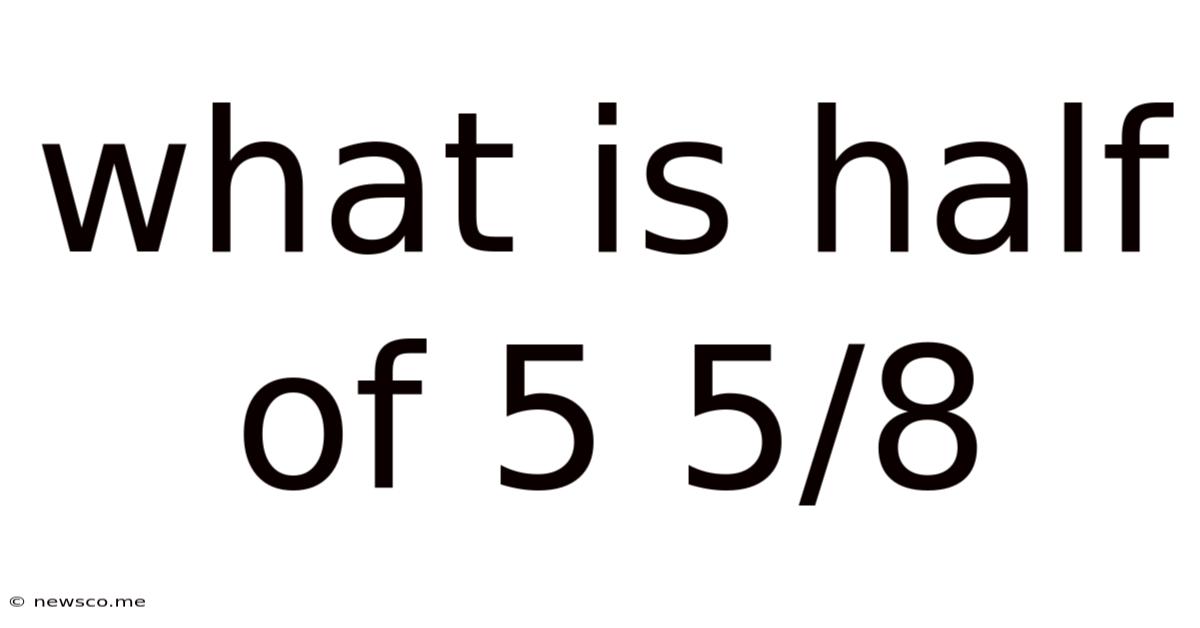
Table of Contents
What is Half of 5 5/8? A Comprehensive Guide to Fraction Division
This seemingly simple question, "What is half of 5 5/8?", opens the door to a deeper understanding of fraction manipulation, a fundamental skill in mathematics with wide-ranging applications in various fields. This article will not only answer the question directly but also delve into the methods and reasoning behind the calculation, providing a comprehensive guide for both beginners and those looking to refresh their fractional arithmetic skills.
Understanding Fractions: A Quick Refresher
Before diving into the calculation, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 5/8, the numerator is 5 and the denominator is 8. This means we have 5 out of 8 equal parts.
Converting Mixed Numbers to Improper Fractions
Our problem involves a mixed number, 5 5/8. A mixed number combines a whole number and a fraction. To perform calculations efficiently, it's often advantageous to convert mixed numbers into improper fractions. An improper fraction is one where the numerator is larger than or equal to the denominator.
To convert 5 5/8 to an improper fraction, follow these steps:
- Multiply the whole number by the denominator: 5 * 8 = 40
- Add the numerator to the result: 40 + 5 = 45
- Keep the same denominator: 8
Therefore, 5 5/8 is equivalent to the improper fraction 45/8.
Finding Half: Division by Two
Finding half of a number is essentially dividing it by 2. In our case, we need to find half of 45/8. This translates to the following division problem:
(45/8) / 2
Methods for Dividing Fractions
There are several ways to approach dividing fractions. Here are two common methods:
Method 1: Reciprocal Multiplication
Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is obtained by swapping its numerator and denominator. The reciprocal of 2 (or 2/1) is 1/2.
So, our problem becomes:
(45/8) * (1/2)
To multiply fractions, multiply the numerators together and the denominators together:
(45 * 1) / (8 * 2) = 45/16
Method 2: Converting to a Common Denominator
Another method involves converting both fractions to have a common denominator before dividing. In this case, we can rewrite 2 as 16/8:
(45/8) / (16/8)
When dividing fractions with the same denominator, you can simply divide the numerators:
45/16
Converting the Improper Fraction Back to a Mixed Number
The result, 45/16, is an improper fraction. To express it as a more understandable mixed number, we perform the division:
45 ÷ 16 = 2 with a remainder of 13
This means that 45/16 is equivalent to 2 13/16.
Therefore, half of 5 5/8 is $\boxed{2\frac{13}{16}}$
Practical Applications of Fraction Division
The ability to divide fractions is crucial in various real-world scenarios:
- Cooking and Baking: Scaling recipes up or down requires accurate fraction division.
- Sewing and Crafts: Calculating fabric or material requirements often involves fractions.
- Construction and Engineering: Precise measurements and calculations frequently involve fractions.
- Finance: Dividing shares or calculating portions of investments often require fractional arithmetic.
Troubleshooting Common Fraction Mistakes
Many students struggle with fractions. Here are some common mistakes to avoid:
- Incorrectly converting mixed numbers: Always double-check your conversion from mixed numbers to improper fractions.
- Forgetting reciprocal multiplication: Remember that dividing by a fraction is the same as multiplying by its reciprocal.
- Incorrect multiplication/division of numerators and denominators: Carefully multiply the numerators and denominators separately.
- Leaving the answer as an improper fraction: It's often clearer to convert improper fractions to mixed numbers for easier interpretation.
Expanding Your Fraction Skills
Mastering fraction division is a building block for more advanced mathematical concepts. Here are some areas to explore further:
- Adding and Subtracting Fractions: Practice operations with different denominators using the least common multiple (LCM).
- Multiplying and Dividing Mixed Numbers: Continue practicing with different types of fraction problems.
- Working with Decimals: Learn to convert between fractions and decimals for versatility in calculations.
- Solving Word Problems: Apply your fraction skills to practical real-world scenarios.
Conclusion
This detailed guide has demonstrated how to calculate half of 5 5/8, highlighting the steps involved in converting mixed numbers, dividing fractions using different methods, and converting back to a mixed number. By understanding the underlying principles and practicing regularly, you'll build confidence and competence in handling fractions, a valuable skill applicable across numerous domains. Remember to practice regularly and seek additional resources if needed to further solidify your understanding of fractional arithmetic. The journey to mastering fractions is one of practice and patience, but the rewards are substantial.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is Half Of 5 5/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.