What Is Larger 3/4 Or 7/8
News Co
May 08, 2025 · 6 min read
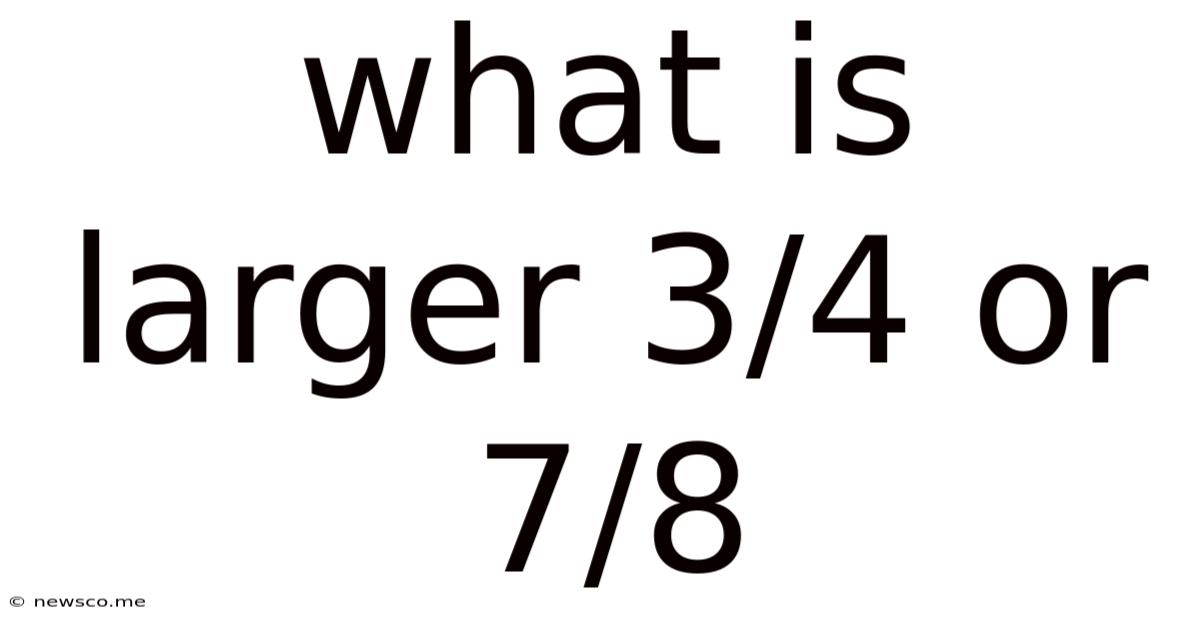
Table of Contents
What's Larger: 3/4 or 7/8? A Deep Dive into Fraction Comparison
Determining which fraction is larger, 3/4 or 7/8, might seem like a simple task, especially for those comfortable with fractions. However, understanding the underlying principles and exploring different methods of comparison offers a valuable opportunity to solidify our understanding of fractional arithmetic and lay a strong foundation for more complex mathematical concepts. This article will delve into multiple approaches to solve this problem, explaining the reasoning behind each method and highlighting their broader applications.
Understanding Fractions: A Quick Refresher
Before we dive into comparing 3/4 and 7/8, let's refresh our understanding of what fractions represent. A fraction, such as a/b, represents a part of a whole. The number 'a' is called the numerator, representing the number of parts we have, and the number 'b' is called the denominator, representing the total number of equal parts the whole is divided into.
Key Concepts:
- Proper Fractions: Fractions where the numerator is smaller than the denominator (e.g., 3/4, 7/8). These fractions represent values less than 1.
- Improper Fractions: Fractions where the numerator is larger than or equal to the denominator (e.g., 5/4, 8/8). These fractions represent values greater than or equal to 1.
- Mixed Numbers: A combination of a whole number and a proper fraction (e.g., 1 1/4). These represent values greater than 1.
Method 1: Finding a Common Denominator
This is perhaps the most common and straightforward method for comparing fractions. The core idea is to rewrite both fractions so they share the same denominator. This allows for a direct comparison of the numerators.
Steps:
-
Find the Least Common Multiple (LCM): The LCM of the denominators 4 and 8 is 8. This means we'll rewrite both fractions with a denominator of 8.
-
Rewrite the Fractions:
- 3/4 can be rewritten as 6/8 (multiply both numerator and denominator by 2).
- 7/8 remains as 7/8.
-
Compare the Numerators: Now that both fractions have the same denominator, we simply compare their numerators: 6 < 7.
-
Conclusion: Therefore, 6/8 (or 3/4) is smaller than 7/8. 7/8 is the larger fraction.
This method emphasizes the importance of equivalent fractions – fractions that represent the same value but have different numerators and denominators. Understanding equivalent fractions is crucial for various mathematical operations, including addition and subtraction of fractions.
Method 2: Visual Representation
Visualizing fractions using diagrams or models can be particularly helpful, especially for beginners. This method aids in intuitive understanding and can reinforce the concept of fractional parts.
Steps:
-
Draw Two Identical Shapes: Draw two identical shapes, such as circles or rectangles.
-
Divide and Shade:
- Divide the first shape into 4 equal parts and shade 3 of them (representing 3/4).
- Divide the second shape into 8 equal parts and shade 7 of them (representing 7/8).
-
Visual Comparison: By visually comparing the shaded areas, it becomes clear that the area shaded in the second shape (7/8) is larger than the area shaded in the first shape (3/4).
-
Conclusion: Therefore, 7/8 is larger than 3/4.
This method provides a strong visual anchor for grasping the concept of fraction comparison. It's especially useful for younger learners or anyone who benefits from visual aids.
Method 3: Converting to Decimals
Converting fractions to decimals offers another approach to comparing them. This method leverages our familiarity with decimal numbers and their ordering.
Steps:
-
Convert to Decimals:
- 3/4 = 0.75 (divide 3 by 4)
- 7/8 = 0.875 (divide 7 by 8)
-
Compare Decimals: Comparing 0.75 and 0.875 is straightforward: 0.75 < 0.875.
-
Conclusion: Therefore, 7/8 is larger than 3/4.
This method showcases the interchangeability between fractions and decimals, a fundamental concept in mathematics. It also highlights the versatility of different numerical representations.
Method 4: Using Number Lines
A number line provides a visual representation of the relative positions of numbers, including fractions. Plotting the fractions on a number line allows for a clear comparison.
Steps:
-
Create a Number Line: Draw a number line from 0 to 1.
-
Divide and Mark: Divide the number line into equal parts representing the denominators of the fractions. For 3/4, divide the line into four equal parts. For 7/8, divide it into eight equal parts.
-
Plot the Fractions: Mark the points corresponding to 3/4 and 7/8 on the number line.
-
Visual Comparison: Observe that the point representing 7/8 lies to the right of the point representing 3/4.
-
Conclusion: Therefore, 7/8 is larger than 3/4.
This method reinforces the concept of fractions as points on a continuous scale, making it particularly useful for visualizing the relative magnitudes of fractions.
Extending the Understanding: Working with More Complex Fractions
The methods described above can be applied to compare any two fractions, regardless of their complexity. Let's consider an example: comparing 5/6 and 11/12.
Using the common denominator method, we find the LCM of 6 and 12, which is 12. We rewrite 5/6 as 10/12. Comparing 10/12 and 11/12, we see that 11/12 is larger.
Using the decimal conversion method, we get 5/6 ≈ 0.833 and 11/12 ≈ 0.917. Again, 11/12 is larger.
The key takeaway is that the chosen method depends largely on personal preference and the context of the problem. However, understanding the underlying principles of fractions is vital for successful comparison.
Real-World Applications of Fraction Comparison
The ability to compare fractions is essential in various real-world applications:
-
Cooking and Baking: Following recipes often involves precise measurements using fractions of cups or teaspoons. Understanding which fraction is larger ensures accurate ingredient proportions.
-
Construction and Engineering: Precision in construction and engineering projects relies on accurate measurements and calculations involving fractions. Comparing fractions is crucial for ensuring that components fit together correctly.
-
Finance and Budgeting: Managing personal finances often involves working with fractions of money, such as calculating discounts or interest rates.
-
Data Analysis: In data analysis, interpreting data presented in fractions or proportions requires a thorough understanding of fraction comparison.
Conclusion: Mastering Fraction Comparison
Comparing fractions, while seemingly basic, forms a cornerstone of mathematical understanding. Mastering this skill opens doors to more advanced mathematical concepts and is invaluable in numerous real-world scenarios. The methods discussed in this article—finding a common denominator, visual representation, decimal conversion, and using number lines—offer a diverse range of approaches, allowing individuals to choose the method that best suits their learning style and problem-solving preferences. By consistently practicing these methods, you'll build a strong foundation in fractions and confidently tackle more complex mathematical challenges. Remember, understanding the "why" behind the methods is just as important as knowing the "how." This deeper understanding will empower you to solve a wider range of problems and appreciate the elegance and power of mathematical principles.
Latest Posts
Latest Posts
-
3 Ten Thousands 5 Hundreds 1 One
May 08, 2025
-
What Is The Degree Measure Of Jkl
May 08, 2025
-
How Many Years Is A Quadrillion Seconds
May 08, 2025
-
How Do You Factor A Third Degree Polynomial
May 08, 2025
-
How To Subtract Mixed Numbers From Whole Numbers
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is Larger 3/4 Or 7/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.