What Is Lcm Of 10 And 4
News Co
Mar 30, 2025 · 5 min read
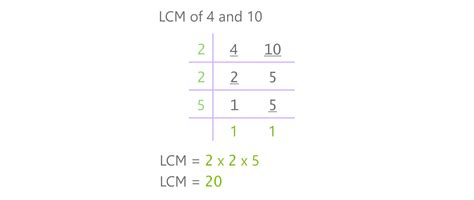
Table of Contents
What is the LCM of 10 and 4? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly in arithmetic and number theory. It's a skill used extensively in various fields, from simplifying fractions to solving complex algebraic equations. This article will delve into the meaning of LCM, explore different methods for calculating it, and provide a detailed explanation of how to find the LCM of 10 and 4. We'll also explore the broader applications of LCM in real-world scenarios.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that is a multiple of all the given numbers. For example, the multiples of 2 are 2, 4, 6, 8, 10, 12… and the multiples of 3 are 3, 6, 9, 12, 15… The common multiples of 2 and 3 are 6, 12, 18… and the least common multiple is 6.
Key characteristics of LCM:
- Positive Integer: The LCM is always a positive integer.
- Divisibility: The LCM is divisible by all the numbers involved.
- Smallest Value: It's the smallest number that satisfies the divisibility condition.
Methods for Calculating LCM
Several methods exist for calculating the LCM, each with its own advantages and disadvantages. Let's explore the most common ones:
1. Listing Multiples Method
This is the most straightforward method, especially for smaller numbers. It involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
Example: Finding the LCM of 2 and 3.
- Multiples of 2: 2, 4, 6, 8, 10, 12…
- Multiples of 3: 3, 6, 9, 12, 15…
- Common multiples: 6, 12, 18…
- LCM(2, 3) = 6
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
Steps:
- Prime Factorization: Find the prime factorization of each number.
- Identify Prime Factors: List all the prime factors involved in the factorizations.
- Highest Powers: Take the highest power of each prime factor.
- Multiply: Multiply the highest powers together. The result is the LCM.
Example: Finding the LCM of 12 and 18.
-
Prime Factorization:
- 12 = 2² × 3
- 18 = 2 × 3²
-
Prime Factors: The prime factors are 2 and 3.
-
Highest Powers: The highest power of 2 is 2², and the highest power of 3 is 3².
-
Multiply: 2² × 3² = 4 × 9 = 36. Therefore, LCM(12, 18) = 36.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula is:
LCM(a, b) = (|a × b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- GCD(a, b) is the greatest common divisor of a and b. The GCD can be found using methods like the Euclidean algorithm.
Example: Finding the LCM of 10 and 4 using the GCD method.
-
GCD(10, 4): Using the Euclidean algorithm:
- 10 = 2 × 4 + 2
- 4 = 2 × 2 + 0
- The GCD is 2.
-
LCM(10, 4): (10 × 4) / 2 = 40 / 2 = 20
Therefore, LCM(10, 4) = 20
Calculating the LCM of 10 and 4: A Detailed Walkthrough
Let's use the three methods discussed above to calculate the LCM of 10 and 4.
1. Listing Multiples Method:
- Multiples of 10: 10, 20, 30, 40, 50…
- Multiples of 4: 4, 8, 12, 16, 20, 24…
- The smallest common multiple is 20.
- Therefore, LCM(10, 4) = 20
2. Prime Factorization Method:
-
Prime Factorization:
- 10 = 2 × 5
- 4 = 2²
-
Prime Factors: The prime factors are 2 and 5.
-
Highest Powers: The highest power of 2 is 2², and the highest power of 5 is 5.
-
Multiply: 2² × 5 = 4 × 5 = 20. Therefore, LCM(10, 4) = 20
3. GCD Method:
-
GCD(10, 4): Using the Euclidean algorithm:
- 10 = 2 × 4 + 2
- 4 = 2 × 2 + 0
- The GCD is 2.
-
LCM(10, 4): (10 × 4) / 2 = 40 / 2 = 20. Therefore, LCM(10, 4) = 20
As demonstrated by all three methods, the least common multiple of 10 and 4 is 20.
Real-World Applications of LCM
The concept of LCM finds numerous practical applications in various fields:
-
Scheduling: Determining when events will occur simultaneously. For example, if two buses arrive at a stop every 10 minutes and 4 minutes respectively, the LCM helps determine when they'll arrive together.
-
Fraction Operations: Finding the least common denominator (LCD) when adding or subtracting fractions requires finding the LCM of the denominators.
-
Measurement Conversions: Converting between different units of measurement often involves using LCM.
-
Project Management: Coordinating tasks with different durations.
-
Music Theory: Determining the least common multiple of note durations to synchronize musical rhythms.
Conclusion: Mastering LCM for Mathematical Success
Understanding and calculating the least common multiple is a crucial skill in mathematics with far-reaching applications. Whether you're using the listing multiples method, the prime factorization method, or the GCD method, the ability to efficiently determine the LCM allows for the solving of a variety of mathematical problems and real-world scenarios. This comprehensive guide has provided a solid foundation for mastering this important concept. Remember to practice regularly to build fluency and confidence in calculating LCMs. The more you work with this concept, the more intuitive it will become, making it a valuable tool in your mathematical arsenal. The example of finding the LCM of 10 and 4, demonstrated through multiple approaches, serves as a practical illustration of the core principles involved.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is Lcm Of 10 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.