What Is One Third Of 12
News Co
Apr 06, 2025 · 5 min read
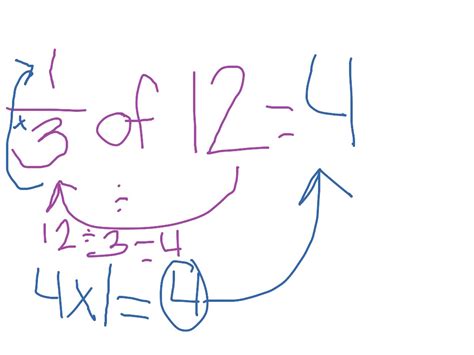
Table of Contents
What is One Third of 12? A Deep Dive into Fractions and Their Applications
This seemingly simple question, "What is one third of 12?", opens the door to a fascinating exploration of fractions, their practical applications, and the fundamental concepts of mathematics. While the answer itself is straightforward (4), the journey to understanding how we arrive at that answer, and the broader implications of fractional calculations, is far more enriching. This article will delve into the intricacies of fractions, demonstrating various methods for solving this problem and showcasing the relevance of fractional arithmetic in everyday life and beyond.
Understanding Fractions: The Building Blocks of Calculation
Before we tackle the problem of finding one-third of 12, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts we are considering.
In our case, "one-third" is represented as the fraction 1/3. The denominator, 3, tells us the whole is divided into three equal parts. The numerator, 1, tells us we are interested in only one of those parts.
Visualizing One-Third
Imagine a pizza cut into three equal slices. One-third of the pizza would be one of those slices. This visual representation helps solidify the concept of a fraction. Similarly, consider a chocolate bar divided into three equal pieces. One-third of the chocolate bar is a single piece. These concrete examples make abstract mathematical concepts more relatable and easier to grasp.
Calculating One-Third of 12: Multiple Approaches
Now, let's address the central question: What is one-third of 12? We can approach this problem using several methods:
Method 1: Division
The most straightforward approach is to divide 12 by 3:
12 ÷ 3 = 4
This directly gives us the answer: one-third of 12 is 4. This method highlights the core relationship between fractions and division. Finding a fraction of a number is essentially dividing that number by the denominator of the fraction.
Method 2: Fraction Multiplication
Another method involves expressing the problem as a multiplication equation:
(1/3) * 12 = ?
To solve this, we multiply the numerator (1) by 12 and then divide the result by the denominator (3):
(1 * 12) / 3 = 12 / 3 = 4
This method reinforces the understanding that finding a fraction of a number is equivalent to multiplying the number by the fraction.
Method 3: Repeated Subtraction
A less conventional but equally valid approach is repeated subtraction. We can repeatedly subtract one-third (which we'll represent as 4 initially – since we know 12/3 = 4) from 12 until we reach zero:
12 - 4 = 8 8 - 4 = 4 4 - 4 = 0
Since we subtracted 4 three times, each subtraction representing one-third of 12, the answer is indeed 4. This method illustrates the concept of fractions as iterative processes of partitioning.
The Significance of Fractions in Everyday Life
The concept of fractions extends far beyond simple mathematical problems. Fractions are integral to numerous aspects of daily life:
-
Cooking and Baking: Recipes frequently involve fractions (e.g., 1/2 cup of sugar, 2/3 cup of flour). Understanding fractions ensures accurate measurements and successful culinary outcomes.
-
Shopping and Budgeting: Sales and discounts are often expressed as fractions (e.g., 1/3 off). Being able to calculate these discounts is crucial for making informed purchasing decisions and managing personal finances effectively.
-
Measurement and Construction: Many measurement systems incorporate fractions (e.g., inches, feet). Carpenters, engineers, and other professionals rely heavily on fraction calculations for precision and accuracy in their work.
-
Time Management: We often think of time in fractional terms (e.g., half an hour, a quarter of a day). Efficient time management depends on an understanding of fractional durations.
-
Data Analysis: Fractions and percentages (which are closely related to fractions) play a significant role in data representation and interpretation. Understanding fractions is crucial for making sense of statistical information and graphs.
Expanding on the Concept: Beyond One-Third
While we've focused on finding one-third of 12, the principles discussed apply to calculating any fraction of any number. Let's explore some variations:
-
Finding Two-Thirds of 12: To find two-thirds (2/3) of 12, we can use the same methods:
- Division: (12 ÷ 3) * 2 = 8
- Multiplication: (2/3) * 12 = (2 * 12) / 3 = 24 / 3 = 8
-
Finding One-Fourth of 12: To find one-fourth (1/4) of 12, we divide 12 by 4:
12 ÷ 4 = 3
-
Finding Three-Quarters of 12: To find three-quarters (3/4) of 12:
- (12 ÷ 4) * 3 = 9
- (3/4) * 12 = (3 * 12) / 4 = 36 / 4 = 9
These examples illustrate the versatility and broad applicability of fraction calculations.
Advanced Applications of Fractions: Algebra and Calculus
Fractions are not confined to elementary arithmetic. They are fundamental building blocks in more advanced mathematical fields like algebra and calculus. For example:
-
Algebraic Equations: Solving algebraic equations often involves working with fractions and manipulating them to isolate variables.
-
Calculus: Derivatives and integrals, central concepts in calculus, rely heavily on the manipulation and understanding of fractions.
-
Probability and Statistics: Fractions are used extensively in probability theory and statistical analysis to represent probabilities and proportions.
Conclusion: The Enduring Importance of Fractions
The seemingly simple question of "What is one-third of 12?" has led us on a journey through the world of fractions, highlighting their importance in various aspects of life. While the answer itself is easily obtained (4), the process of understanding the underlying concepts and applying different calculation methods offers valuable insights into the fundamental principles of mathematics and their pervasive influence on our daily lives. Mastering fractions is not merely about solving arithmetic problems; it's about developing a crucial skill set that underpins success in various fields and enhances our ability to navigate and interpret the quantitative world around us. From simple recipes to complex mathematical equations, fractions remain an essential element in our quantitative understanding of the world.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is One Third Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.