What Is Prime Factorization Of 63
News Co
Apr 08, 2025 · 5 min read
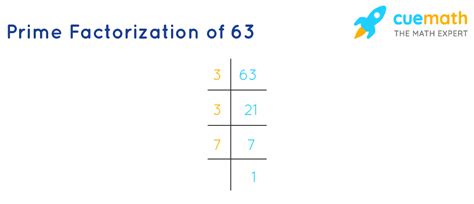
Table of Contents
What is Prime Factorization of 63? A Deep Dive into Number Theory
Prime factorization, a cornerstone of number theory, is the process of breaking down a composite number into its prime number components. Understanding this process unlocks a wealth of mathematical possibilities, from simplifying fractions to solving complex cryptographic problems. This article will delve into the prime factorization of 63, explaining the method, its applications, and exploring related concepts within number theory.
Understanding Prime Numbers and Composite Numbers
Before we tackle the prime factorization of 63, let's clarify some fundamental concepts:
Prime Numbers: The Building Blocks
A prime number is a natural number greater than 1 that has only two distinct positive divisors: 1 and itself. In essence, it's indivisible by any other number except 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. Prime numbers are the fundamental building blocks of all other integers.
Composite Numbers: Products of Primes
A composite number is a positive integer that has at least one divisor other than 1 and itself. In simpler terms, it's a number that can be formed by multiplying two smaller positive integers. Every composite number can be expressed uniquely as a product of prime numbers. This unique representation is known as its prime factorization.
Finding the Prime Factorization of 63
Now, let's find the prime factorization of 63. We can employ a method called the "factor tree" or repeated division by prime numbers.
Method 1: Factor Tree
- Start with the number 63.
- Find the smallest prime number that divides 63. This is 3.
- Divide 63 by 3: 63 ÷ 3 = 21.
- Now, find the smallest prime number that divides 21. This is also 3.
- Divide 21 by 3: 21 ÷ 3 = 7.
- 7 is a prime number. We've reached the end of our factorization.
The factor tree visually represents this process:
63
/ \
3 21
/ \
3 7
Therefore, the prime factorization of 63 is 3 x 3 x 7, which can be written as 3² x 7.
Method 2: Repeated Division
Alternatively, we can use repeated division by prime numbers:
- Start with 63.
- Divide by the smallest prime number, 3: 63 ÷ 3 = 21.
- Divide the result (21) by the smallest prime number again, 3: 21 ÷ 3 = 7.
- 7 is a prime number. The process ends here.
This confirms that the prime factorization of 63 is 3 x 3 x 7 or 3² x 7.
Applications of Prime Factorization
The seemingly simple concept of prime factorization has far-reaching applications in various fields:
1. Simplifying Fractions:
Prime factorization is crucial for simplifying fractions to their lowest terms. Consider the fraction 63/105. By finding the prime factorization of both the numerator (63 = 3² x 7) and the denominator (105 = 3 x 5 x 7), we can easily cancel out common factors:
63/105 = (3² x 7) / (3 x 5 x 7) = 3/5
2. Finding the Greatest Common Divisor (GCD) and Least Common Multiple (LCM):
Prime factorization is the most efficient method for calculating the GCD and LCM of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder, while the LCM is the smallest number that is a multiple of all the given numbers.
For example, let's find the GCD and LCM of 63 and 105:
- Prime factorization of 63: 3² x 7
- Prime factorization of 105: 3 x 5 x 7
GCD: The common prime factors are 3 and 7. The GCD is 3 x 7 = 21.
LCM: The LCM includes all prime factors, taking the highest power of each: 3² x 5 x 7 = 315.
3. Cryptography:
Prime factorization plays a vital role in modern cryptography, particularly in RSA encryption. RSA relies on the difficulty of factoring the product of two large prime numbers. Breaking RSA encryption essentially involves factoring a very large composite number into its prime components, a computationally intensive task for sufficiently large numbers.
4. Number Theory and Abstract Algebra:
Prime factorization forms the basis of many theorems and concepts in higher-level mathematics, including modular arithmetic, group theory, and ring theory. Understanding prime numbers and their properties is fundamental to advanced mathematical research.
Exploring Related Concepts
Several concepts are closely related to prime factorization and enhance our understanding of number theory:
1. Fundamental Theorem of Arithmetic:
This fundamental theorem states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This unique representation is the core of prime factorization.
2. Sieve of Eratosthenes:
This ancient algorithm provides an efficient way to find all prime numbers up to a specified integer. It's a useful tool for identifying prime factors during factorization.
3. Perfect Numbers:
A perfect number is a positive integer that is equal to the sum of its proper divisors (excluding the number itself). Prime factorization plays a role in understanding and identifying perfect numbers. For example, 6 (2 x 3) is a perfect number (1 + 2 + 3 = 6).
4. Mersenne Primes:
Mersenne primes are prime numbers of the form 2<sup>p</sup> - 1, where 'p' is also a prime number. These primes have a special significance in number theory and are often the focus of extensive computational searches.
Conclusion: The Significance of Prime Factorization
The seemingly simple process of prime factorization of 63 (3² x 7) opens a door to a vast and fascinating world of number theory. Its applications extend far beyond basic arithmetic, playing a critical role in cryptography, simplifying complex calculations, and forming the foundation for advanced mathematical concepts. Understanding prime factorization provides a deeper appreciation for the structure and elegance of the number system, making it an essential concept for anyone interested in mathematics or computer science. By mastering this fundamental technique, we unlock a powerful tool for solving a wide array of mathematical problems and gaining a deeper insight into the fascinating world of numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is Prime Factorization Of 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.