What Is Prime Factorization Of 70
News Co
Apr 05, 2025 · 5 min read
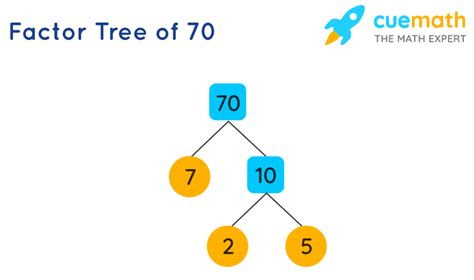
Table of Contents
What is Prime Factorization of 70? A Deep Dive into Number Theory
Prime factorization, a cornerstone of number theory, is the process of finding the prime numbers that multiply together to make a given number. Understanding prime factorization is crucial for various mathematical operations, from simplifying fractions to solving complex equations. This article will delve into the prime factorization of 70, explaining the method, its significance, and related concepts in detail.
Understanding Prime Numbers
Before we tackle the prime factorization of 70, let's clarify what a prime number is. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In simpler terms, it's only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered a prime number. Prime numbers are the building blocks of all other numbers, forming the foundation of arithmetic and number theory.
The Fundamental Theorem of Arithmetic
The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This theorem ensures that the prime factorization of any number is unique, making it a powerful tool in mathematics. For example, the prime factorization of 12 is 2 x 2 x 3, and no other combination of prime numbers will result in 12. This uniqueness is critical for various mathematical proofs and algorithms.
Finding the Prime Factorization of 70
Now, let's find the prime factorization of 70. We can use a method called the factor tree. The factor tree is a visual representation of the process, breaking down the number into its prime factors step-by-step.
-
Start with the number 70: We begin by finding any two factors of 70. A simple pair is 7 and 10.
-
Break down the factors: Now, we need to examine 7 and 10. 7 is a prime number, so we'll circle it. 10 is not prime; it can be factored into 2 and 5. Both 2 and 5 are prime numbers, so we'll circle them.
-
The prime factorization: Our factor tree reveals that the prime factors of 70 are 2, 5, and 7. Therefore, the prime factorization of 70 is 2 x 5 x 7.
Here's a visual representation of the factor tree:
70
/ \
7 10
/ \
2 5
Alternative Methods for Prime Factorization
While the factor tree is a helpful visual method, other techniques can be used to find prime factorizations, particularly for larger numbers.
-
Division by Prime Numbers: This method involves systematically dividing the number by the smallest prime number (2) and continuing with the next prime number (3, 5, 7, and so on) until the result is 1. The prime numbers used in the divisions are the prime factors. For 70:
- 70 ÷ 2 = 35
- 35 ÷ 5 = 7
- 7 ÷ 7 = 1
This confirms that the prime factors of 70 are 2, 5, and 7.
-
Using Algorithms: For very large numbers, specialized algorithms like the Pollard rho algorithm or the general number field sieve are employed to find prime factors efficiently. These algorithms are beyond the scope of this introductory article but are essential for cryptography and other advanced applications.
Applications of Prime Factorization
Prime factorization isn't just a theoretical concept; it has practical applications across various fields:
-
Cryptography: RSA cryptography, a widely used method for secure communication, relies heavily on the difficulty of factoring large numbers into their prime components. The security of encrypted data depends on the inability to quickly factor extremely large numbers.
-
Simplifying Fractions: Finding the prime factorization of the numerator and denominator of a fraction allows for simplification by canceling common factors.
-
Finding the Least Common Multiple (LCM) and Greatest Common Divisor (GCD): Prime factorization is crucial for efficiently calculating the LCM and GCD of two or more numbers. These calculations are fundamental in various mathematical and engineering applications.
-
Number Theory and Abstract Algebra: Prime factorization forms the base for many advanced concepts in number theory and abstract algebra, impacting fields like coding theory and algebraic geometry.
Exploring Further: Prime Factorization and its Extensions
The concept of prime factorization extends beyond integers to other mathematical structures. For instance, in polynomial rings, the concept of irreducible polynomials is analogous to prime numbers. Factoring polynomials into irreducible components has significant applications in algebra and calculus.
The distribution of prime numbers is another fascinating area of research. The Prime Number Theorem, a landmark result in number theory, provides an approximation for the number of primes less than a given number. This theorem highlights the asymptotic behavior of prime numbers, a topic that continues to captivate mathematicians.
Furthermore, the search for larger prime numbers has driven advancements in computational mathematics and algorithm design. The discovery of ever-larger prime numbers, like Mersenne primes, showcases the enduring fascination with prime numbers and their properties.
Conclusion: The Importance of Prime Factorization
The prime factorization of 70, while seemingly simple, underscores a fundamental concept in mathematics. The process of breaking down a number into its prime components provides a unique representation that has wide-ranging implications. From simplifying fractions to securing online transactions, the power of prime factorization extends far beyond its basic application. Understanding this fundamental concept unlocks doors to more advanced mathematical concepts and applications, highlighting its enduring importance in mathematics and computer science. The exploration of prime numbers and their factorization continues to be a rich and rewarding area of study, pushing the boundaries of our understanding of numbers and their properties.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is Prime Factorization Of 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.