What Is Square Root Of 17
News Co
Apr 06, 2025 · 5 min read
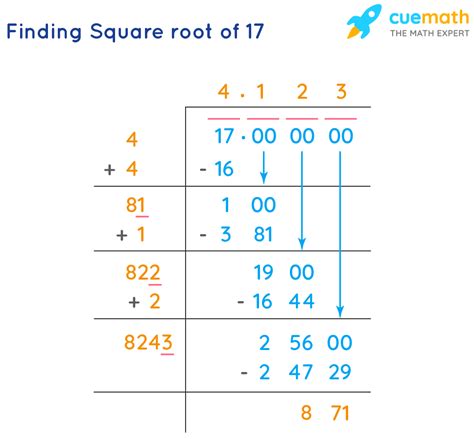
Table of Contents
What is the Square Root of 17? A Deep Dive into Irrational Numbers
The seemingly simple question, "What is the square root of 17?" opens a door to a fascinating world of mathematics, specifically dealing with irrational numbers and their properties. While a quick calculator search will give you a decimal approximation, understanding the true nature of √17 requires a deeper exploration. This article will delve into the intricacies of this specific square root, exploring its properties, calculation methods, and its significance within the broader mathematical landscape.
Understanding Square Roots
Before we tackle the square root of 17, let's establish a foundational understanding of what a square root represents. The square root of a number, denoted as √x, is a value that, when multiplied by itself, equals x. In simpler terms, it's the inverse operation of squaring a number. For example:
- √9 = 3 because 3 * 3 = 9
- √16 = 4 because 4 * 4 = 16
This concept is straightforward for perfect squares – numbers that are the product of an integer multiplied by itself. However, things get more interesting when dealing with non-perfect squares, like 17.
The Irrational Nature of √17
Unlike the square roots of 9 and 16, the square root of 17 is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation is non-terminating and non-repeating, meaning it goes on forever without ever settling into a predictable pattern.
This irrationality is a key characteristic that distinguishes √17 from other square roots. This inherent complexity necessitates exploring different methods to approximate its value and understand its place within the number system.
Methods for Approximating √17
Since we cannot express √17 as a precise fraction or terminating decimal, we rely on approximation methods. Several techniques can be used, each with its own level of accuracy and complexity:
1. Using a Calculator: The Simplest Approach
The most convenient method is to use a calculator. Simply input "√17" and the calculator will provide a decimal approximation, typically accurate to several decimal places. This is a practical approach for everyday calculations, but it doesn't offer a deeper understanding of the number itself. A typical approximation is 4.1231056.
2. The Babylonian Method (or Heron's Method): An Iterative Approach
This ancient method provides a way to iteratively refine an approximation of the square root. It involves an iterative process that progressively gets closer to the true value:
- Start with an initial guess: Let's choose 4, as it's close to the expected value.
- Improve the guess: Divide 17 by the guess (17/4 = 4.25) and average the result with the original guess: (4 + 4.25)/2 = 4.125
- Repeat: Use the new guess (4.125) and repeat step 2. This process can be repeated until the desired level of accuracy is achieved.
This iterative approach demonstrates how we can progressively refine our approximation, showcasing the underlying mathematical principle behind calculating square roots.
3. The Newton-Raphson Method: A More Sophisticated Approach
The Newton-Raphson method is a more advanced iterative technique for finding the roots of a function. Applied to finding √17, it involves the following steps:
- Define a function: Let f(x) = x² - 17. The root of this function is √17.
- Find the derivative: The derivative of f(x) is f'(x) = 2x.
- Iterative formula: The iterative formula for the Newton-Raphson method is: x_(n+1) = x_n - f(x_n) / f'(x_n)
- Iterate: Starting with an initial guess, repeatedly apply the formula until the desired accuracy is achieved.
This method offers faster convergence than the Babylonian method, achieving higher accuracy with fewer iterations.
4. Continued Fractions: An Elegant Representation
Continued fractions provide an elegant way to represent irrational numbers as an infinite sequence of fractions. While the full continued fraction for √17 is infinite, we can truncate it to obtain increasingly accurate approximations. The continued fraction representation of √17 is:
4 + 1/(8 + 1/(8 + 1/(8 + ...)))
By truncating this fraction at different points, we get progressively better rational approximations of √17.
The Significance of √17 in Mathematics
While √17 might seem like a specific and isolated example, its irrational nature and the methods used to approximate it highlight fundamental concepts in mathematics:
- Irrational Numbers: √17's irrationality demonstrates the richness and complexity of the number system, extending beyond rational numbers.
- Approximation Techniques: The methods discussed (Babylonian, Newton-Raphson, continued fractions) illustrate different approaches to approximating values that cannot be expressed exactly.
- Number Theory: The study of irrational numbers and their properties is a central theme in number theory, a branch of mathematics dedicated to the properties of integers.
- Calculus: The Newton-Raphson method is a powerful tool in calculus, used to find solutions to various mathematical problems beyond square root approximations.
Understanding √17, therefore, contributes to a broader mathematical understanding of irrational numbers, approximation techniques, and the elegance of mathematical methods.
Applications of Square Roots
Square roots, including the square root of 17, have widespread applications in various fields:
- Geometry: Calculating distances, areas, and volumes often involves square roots, particularly in Pythagorean theorem applications.
- Physics: Many physical phenomena are described by equations involving square roots, such as calculating velocities and energies.
- Engineering: Design and construction projects frequently utilize square roots in calculations related to structural integrity, stability, and material properties.
- Computer Graphics: Rendering and simulations often utilize square roots to perform calculations related to vector operations and coordinate transformations.
- Finance: Calculating investment returns and evaluating financial models often involve square roots, particularly in determining standard deviations and variances.
Conclusion: Beyond the Decimal Approximation
While a calculator can readily provide a decimal approximation of √17, understanding its nature as an irrational number and the methods used to approximate its value provides a deeper appreciation of the mathematical concepts involved. The exploration of √17 serves as a microcosm of broader mathematical principles, highlighting the elegance and power of mathematical tools and their significance in various scientific and practical fields. It’s more than just a number; it's a gateway to understanding the intricacies of the real number system and the enduring quest for precision in mathematics.
Latest Posts
Latest Posts
-
What Is A 5 8 As A Grade
Apr 07, 2025
-
How Long Is A 40 Mile Drive
Apr 07, 2025
-
26 Degrees Celsius Converted To Fahrenheit
Apr 07, 2025
-
Cuanto Es 30 Grados Fahrenheit En Centigrados
Apr 07, 2025
-
Does Y Or X Come First
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Is Square Root Of 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
