What Is Square Root Of 37
News Co
Apr 06, 2025 · 4 min read
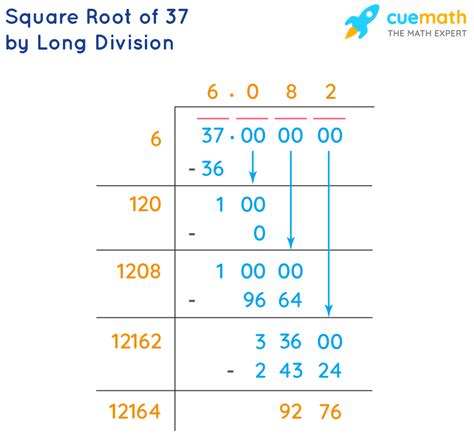
Table of Contents
What is the Square Root of 37? A Deep Dive into Irrational Numbers
The question, "What is the square root of 37?" seems simple enough. However, delving into its answer reveals a fascinating journey into the world of irrational numbers and the intricacies of mathematical calculation. This article will explore various methods of approximating √37, discuss its properties, and touch upon its significance in different mathematical contexts.
Understanding Square Roots
Before we tackle the square root of 37, let's establish a fundamental understanding of square roots. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 * 3 = 9. This is also written as 3².
However, not all numbers have perfect square roots – meaning whole numbers that when squared produce the original number. Numbers like 2, 3, 5, 7, 10, and indeed 37, fall into this category. These numbers have irrational square roots. This means their decimal representation continues infinitely without repeating.
Approximating √37: Methods and Techniques
Since √37 is irrational, we can only approximate its value. Several methods can achieve this, each with varying levels of accuracy and complexity.
1. Using a Calculator
The simplest and most direct method is using a calculator. Most calculators have a square root function (√). Inputting 37 will yield an approximation, typically accurate to several decimal places. A standard calculator might give you approximately 6.08276.
2. The Babylonian Method (or Heron's Method)
This iterative method provides increasingly accurate approximations with each step. It's based on the principle of repeatedly averaging a guess with the result of dividing the number by the guess.
Steps:
- Make an initial guess: Let's start with 6, as it's the closest whole number whose square is less than 37.
- Refine the guess: Divide 37 by the guess (37/6 ≈ 6.1667).
- Average: Average the guess and the result from step 2: (6 + 6.1667)/2 ≈ 6.08335.
- Repeat: Use the average as the new guess and repeat steps 2 and 3. The more iterations you perform, the closer you'll get to the actual value of √37.
Let's perform another iteration:
- 37 / 6.08335 ≈ 6.08276
- (6.08335 + 6.08276) / 2 ≈ 6.083055
As you can see, the approximation is getting increasingly precise.
3. Linear Approximation
This method uses the tangent line to the function f(x) = √x at a nearby point with a known square root. Let's use the point (36, 6) since √36 = 6. The derivative of √x is 1/(2√x).
The equation of the tangent line at x = 36 is:
y - 6 = (1/(2√36)) * (x - 36) => y = (1/12)x + 3
Plugging in x = 37:
y = (1/12)*37 + 3 ≈ 6.0833
While less precise than the Babylonian method, this offers a quick, linear approximation.
4. Numerical Methods (Newton-Raphson Method)
More advanced numerical methods, like the Newton-Raphson method, can achieve high accuracy in fewer iterations. These methods are typically used in computer programs for calculating square roots to many decimal places. These methods rely on calculus and iterative processes to refine approximations.
The Significance of Irrational Numbers: √37 in Context
While we might initially see the irrationality of √37 as a mere inconvenience, it highlights a crucial aspect of mathematics: the existence of numbers that cannot be expressed as a simple fraction. This has broader implications:
-
Geometry: Irrational numbers are essential in geometry. The diagonal of a square with sides of length 1 is √2, an irrational number. Similarly, irrational numbers frequently appear in calculations involving circles and other geometric shapes. The applications of √37 might be found in calculating the length of a diagonal in a specific three-dimensional geometric structure.
-
Trigonometry: Trigonometric functions often produce irrational numbers. Solutions to trigonometric equations may involve irrational square roots, including potentially √37 in certain scenarios.
-
Physics and Engineering: Many physical phenomena and engineering designs involve irrational numbers. Mathematical models used to describe these phenomena often incorporate square roots and irrational numbers. The value might appear in calculations involving vectors or specific physical constants in some engineering or physics applications.
-
Number Theory: Irrational numbers are a major subject of study in number theory. Understanding their properties and relationships contributes to a deeper understanding of mathematics as a whole. Researchers in number theory would explore the properties and relationships of √37 within the context of irrational numbers.
Beyond the Approximation: Understanding the Concept
It's vital to remember that the approximations of √37, no matter how precise, are merely that – approximations. The true value of √37 exists as a non-terminating, non-repeating decimal. This underscores the richness and complexity of the number system and highlights the limitations of our ability to precisely represent certain mathematical concepts.
Conclusion: The Enduring Mystery of √37
The square root of 37, while appearing initially as a simple arithmetic problem, opens a window into the profound world of irrational numbers. It demonstrates the power and limitations of different approximation techniques and underscores the importance of irrational numbers in various fields of mathematics, science, and engineering. Understanding its nature expands our comprehension of the mathematical universe's elegance and complexity. The pursuit of a precise value, though unattainable in decimal form, allows for a deep dive into mathematical concepts and the beautiful intricacies of the number system.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is Square Root Of 37 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.