What Is Square Root Of 40
News Co
Apr 07, 2025 · 5 min read
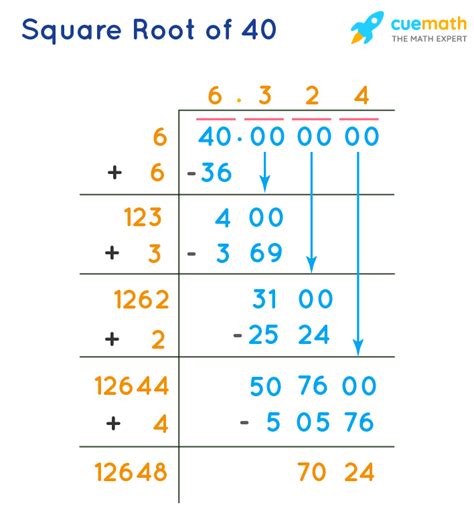
Table of Contents
What is the Square Root of 40? A Deep Dive into Square Roots and Approximations
The seemingly simple question, "What is the square root of 40?" opens a door to a fascinating exploration of mathematical concepts, approximation techniques, and the power of numerical analysis. While a calculator readily provides a decimal approximation, understanding the underlying principles offers a much richer understanding. This article will delve into the intricacies of square roots, explore methods for approximating √40, and discuss the significance of this seemingly basic calculation in broader mathematical contexts.
Understanding Square Roots
Before diving into the specifics of √40, let's establish a solid foundation. The square root of a number 'x' is a value 'y' such that when 'y' is multiplied by itself (y*y or y²), the result is 'x'. In simpler terms, it's the number that, when squared, gives you the original number. For example, the square root of 9 (√9) is 3, because 3 * 3 = 9.
Key Properties of Square Roots:
- Non-negative: The principal square root of a number is always non-negative. While (-3) * (-3) = 9, we typically focus on the positive square root.
- Perfect Squares: Numbers that have whole number square roots are called perfect squares (e.g., 1, 4, 9, 16, 25, etc.).
- Irrational Numbers: Many numbers don't have whole number square roots. Their square roots are irrational numbers, meaning they cannot be expressed as a simple fraction and have an infinite number of non-repeating decimal places. √40 falls into this category.
Calculating the Square Root of 40: Methods and Approximations
Finding the exact square root of 40 is impossible using simple arithmetic. It's an irrational number. However, we can employ several methods to find increasingly accurate approximations:
1. Prime Factorization and Simplification
The first step in understanding √40 involves prime factorization. We break down 40 into its prime factors: 40 = 2 x 2 x 2 x 5 = 2² x 2 x 5. This allows us to simplify the square root:
√40 = √(2² x 2 x 5) = √2² x √(2 x 5) = 2√10
This simplifies the expression, but we still need to approximate √10.
2. Using a Calculator
The most straightforward method is using a calculator or computer software. This will provide a decimal approximation:
√40 ≈ 6.32455532
This is accurate to several decimal places, sufficient for most practical applications.
3. Babylonian Method (or Heron's Method)
This iterative method provides increasingly accurate approximations. It starts with an initial guess and refines it through successive iterations:
- Initial Guess: Let's start with a guess of 6 (since 6² = 36, which is close to 40).
- Iteration: The formula for the Babylonian method is: xₙ₊₁ = ½ * (xₙ + (a/xₙ)), where 'a' is the number whose square root we're finding (40 in this case), and 'xₙ' is the current guess.
- Repeat: We repeat step 2 until the desired level of accuracy is reached.
Let's perform a few iterations:
- Iteration 1: x₁ = ½ * (6 + (40/6)) ≈ 6.333
- Iteration 2: x₂ = ½ * (6.333 + (40/6.333)) ≈ 6.3246
- Iteration 3: x₃ = ½ * (6.3246 + (40/6.3246)) ≈ 6.324555
As you can see, the approximation converges rapidly towards the calculator's result.
4. Linear Approximation
This method uses the tangent line to the function f(x) = √x at a nearby point to estimate the value. Let's use the point x=36 (√36 = 6):
The derivative of √x is 1/(2√x). At x=36, the derivative is 1/(2*6) = 1/12.
The equation of the tangent line is: y - 6 = (1/12)(x - 36)
To approximate √40, we substitute x = 40:
y - 6 = (1/12)(40 - 36) = 1/3
y ≈ 6 + 1/3 ≈ 6.333
This method provides a less precise approximation than the Babylonian method, but it's conceptually simpler.
The Significance of √40 in Mathematical Contexts
While √40 might seem like a simple calculation, it appears in various mathematical contexts:
- Geometry: It could represent the length of the diagonal of a rectangle or the hypotenuse of a right-angled triangle. Pythagorean theorem applications frequently involve such calculations.
- Trigonometry: Square roots are crucial in trigonometric calculations, particularly when dealing with angles and unit circles.
- Calculus: Square roots appear in many calculus problems, including integration and differentiation.
- Physics and Engineering: Many physical laws and engineering calculations involve square roots. Examples include calculating velocity, acceleration, and energy.
Beyond the Calculation: Exploring Related Concepts
Understanding √40 goes beyond simply finding its numerical value. It encourages exploration of broader mathematical ideas:
- Number Systems: The calculation highlights the distinction between rational and irrational numbers.
- Approximation Techniques: It demonstrates the power of various numerical methods for approximating solutions when exact solutions are unavailable.
- Computational Complexity: The Babylonian method illustrates the concept of iterative algorithms and their convergence rates.
- Error Analysis: Comparing different approximation methods allows for an exploration of error analysis – understanding the magnitude of the error in different approximation techniques.
Conclusion: The Beauty of Approximation
The question of what the square root of 40 is, initially a seemingly basic arithmetic problem, opens a window into a rich world of mathematical concepts and techniques. While a calculator offers a quick decimal approximation, understanding the underlying principles and applying various approximation methods provides a deeper and more insightful understanding of square roots and their significance in mathematics and beyond. The journey of approximation itself reveals the beauty and power of numerical analysis in handling problems where exact solutions are elusive. This exploration serves as a reminder of the elegance and intricacy residing within seemingly simple mathematical questions.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is Square Root Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.