What Is Square Root Of 41
News Co
Apr 06, 2025 · 4 min read
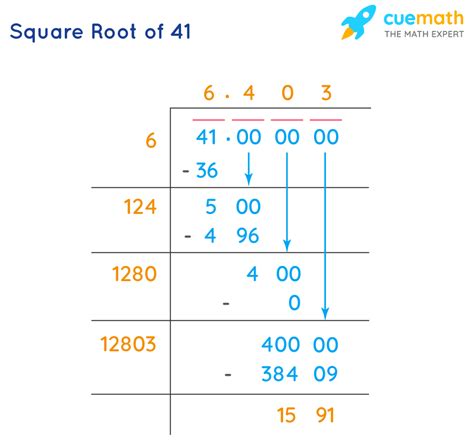
Table of Contents
What is the Square Root of 41? A Deep Dive into Irrational Numbers and Approximation Methods
The seemingly simple question, "What is the square root of 41?", opens a fascinating window into the world of mathematics, specifically the realm of irrational numbers and numerical approximation techniques. While a precise, finite decimal representation doesn't exist, understanding how to approach this problem reveals powerful concepts applicable far beyond this single calculation.
Understanding Square Roots and Irrational Numbers
Before delving into the specifics of √41, let's establish a foundational understanding. The square root of a number (x) is a value that, when multiplied by itself, equals x. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. This is a perfect square; its square root is a whole number.
However, not all numbers are perfect squares. Numbers like 41, when subjected to a square root operation, yield irrational numbers. Irrational numbers cannot be expressed as a simple fraction (a ratio of two integers) and their decimal representations extend infinitely without repeating. This means we can only approximate √41, not find its exact value.
Methods for Approximating √41
Several methods exist for approximating the square root of 41. Let's explore some of the most common and effective approaches:
1. The Babylonian Method (or Heron's Method)
This iterative method refines an initial guess to achieve increasingly accurate approximations. The formula is:
x_(n+1) = 0.5 * (x_n + (N/x_n))
Where:
- x_n is the current approximation
- x_(n+1) is the next, improved approximation
- N is the number whose square root we seek (in our case, 41)
Let's illustrate with an initial guess of 6 (since 6 x 6 = 36, which is close to 41):
- Iteration 1: x_1 = 0.5 * (6 + (41/6)) ≈ 6.4167
- Iteration 2: x_2 = 0.5 * (6.4167 + (41/6.4167)) ≈ 6.4031
- Iteration 3: x_3 = 0.5 * (6.4031 + (41/6.4031)) ≈ 6.4031
As you can see, the method converges rapidly. After just a few iterations, we obtain a highly accurate approximation of √41 ≈ 6.4031.
2. Using a Calculator or Computer Software
Modern calculators and computer software incorporate sophisticated algorithms, often variations of the Babylonian method or other advanced techniques, to calculate square roots with high precision. These tools provide a quick and convenient way to obtain an approximation, often displaying many decimal places. For √41, a calculator will typically show a value around 6.40312423743.
3. Linear Approximation
This simpler method uses the concept of linear interpolation. We find two perfect squares that bracket 41—36 (6²) and 49 (7²). Then we can approximate √41 by linearly interpolating between these values:
Since 41 is 5 units away from 36 (41 - 36 = 5) and 8 units away from 49 (49 - 41 = 8), we can approximate:
√41 ≈ 6 + (5/13) ≈ 6.38
This method is less accurate than the Babylonian method, but it illustrates a fundamental concept of approximation using known values.
4. Taylor Series Expansion
For those with a background in calculus, the Taylor series expansion provides a powerful way to approximate functions, including square roots. The Taylor series for √(1+x) around x=0 is:
√(1+x) ≈ 1 + (1/2)x - (1/8)x² + (1/16)x³ - ...
To use this for √41, we rewrite it as √(36 + 5) = 6√(1 + 5/36). Substituting x = 5/36 into the Taylor series and performing the calculation (considering several terms for accuracy) provides a reasonably accurate approximation. This method requires a solid understanding of calculus and series convergence.
The Significance of Irrational Numbers
The fact that √41 is irrational highlights a crucial aspect of the number system. While rational numbers (fractions) can precisely represent many quantities, irrational numbers demonstrate that the number line is densely populated with values beyond simple ratios. Irrational numbers are fundamental to geometry (e.g., the diagonal of a unit square is √2), calculus, and many other areas of mathematics.
Practical Applications
Although the exact value of √41 is elusive, approximations are sufficient for most real-world applications. For example:
- Engineering and Physics: Calculations involving lengths, areas, and volumes often require square root operations. Approximations within a reasonable error margin suffice for many engineering problems.
- Computer Graphics: Generating smooth curves and shapes in computer graphics often utilizes square root calculations as part of mathematical transformations.
- Financial Modeling: Some financial models incorporate square root calculations in risk assessment and portfolio optimization.
Conclusion: Beyond the Number Itself
The quest to determine the square root of 41 isn't just about finding a specific numerical value. It's about understanding the nature of numbers, the limitations of representation, and the power of approximation techniques. The journey of exploring different approximation methods enhances mathematical understanding and problem-solving skills, extending far beyond this single example. Each method offers a unique perspective on how we approach and grapple with irrational numbers, demonstrating the rich tapestry woven by the seemingly simple question: What is the square root of 41? The answer, while always an approximation, unlocks a deeper understanding of the mathematical world.
Latest Posts
Latest Posts
-
How Many Inches In One Square Foot
Apr 08, 2025
-
What Are The Factors For 93
Apr 08, 2025
-
Cuanto Es 20 Grados Centigrados En Fahrenheit
Apr 08, 2025
-
What Are All The Factors Of 92
Apr 08, 2025
-
What Is The Least Common Multiple Of 12 And 7
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is Square Root Of 41 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.