What Is The Absolute Value Of 16
News Co
Apr 27, 2025 · 6 min read
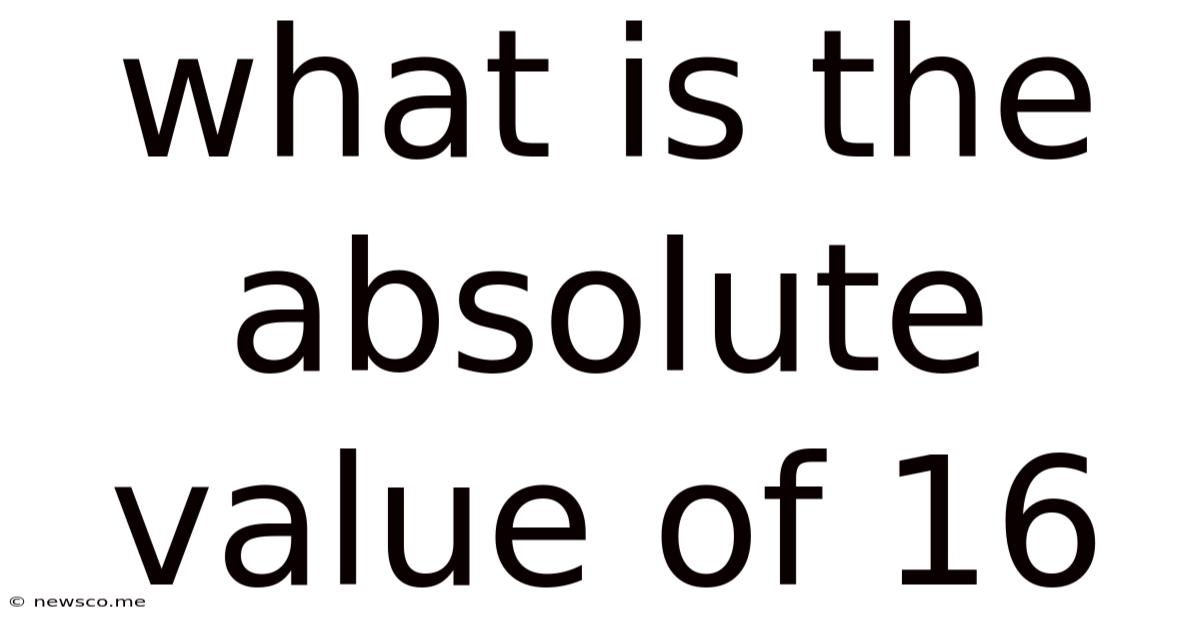
Table of Contents
What is the Absolute Value of 16? A Deep Dive into Absolute Value and its Applications
The seemingly simple question, "What is the absolute value of 16?" opens a door to a fascinating exploration of a fundamental concept in mathematics: absolute value. While the answer itself is straightforward (it's 16!), understanding the concept's implications and applications extends far beyond this single calculation. This article will delve into the definition of absolute value, its properties, diverse applications, and its significance in various fields. We'll also tackle some common misconceptions and explore related mathematical concepts.
Understanding Absolute Value: A Formal Definition
The absolute value of a number is its distance from zero on the number line. This distance is always non-negative, regardless of whether the number itself is positive or negative. Formally, the absolute value of a number x, denoted as |x|, is defined as follows:
- If x ≥ 0, then |x| = x (The absolute value of a non-negative number is the number itself.)
- If x < 0, then |x| = -x (The absolute value of a negative number is its opposite, which is positive.)
Let's illustrate this with a few examples:
- |16| = 16 (16 is non-negative, so its absolute value is 16.)
- |-16| = 16 (-16 is negative, so its absolute value is -(-16) = 16.)
- |0| = 0 (The absolute value of zero is zero.)
- |5.7| = 5.7
- |-2.3| = 2.3
The key takeaway is that the absolute value function always returns a non-negative value. It essentially "strips" away the negative sign if one is present.
Properties of Absolute Value: A Mathematical Toolkit
The absolute value function possesses several important properties that are crucial for various mathematical operations and problem-solving:
- Non-negativity: |x| ≥ 0 for all real numbers x.
- Even function: |x| = |-x| for all real numbers x. This symmetry around the y-axis is a defining characteristic.
- Multiplicative property: |xy| = |x||y| for all real numbers x and y. The absolute value of a product is the product of the absolute values.
- Triangle inequality: |x + y| ≤ |x| + |y| for all real numbers x and y. This inequality is fundamental in various areas of mathematics, including analysis and linear algebra. It essentially states that the absolute value of a sum is less than or equal to the sum of the absolute values.
- Absolute value equations and inequalities: Solving equations and inequalities involving absolute values requires careful consideration of the definition and properties mentioned above. For example, solving |x - 3| = 5 involves considering two separate cases: x - 3 = 5 and -(x - 3) = 5.
Applications of Absolute Value: Beyond the Classroom
The concept of absolute value isn't confined to theoretical mathematics; it finds practical applications in numerous fields:
1. Physics and Engineering: Measuring Distance and Displacement
In physics, absolute value is crucial for representing distance and displacement. Distance is always a non-negative quantity, representing the total ground covered, regardless of direction. Displacement, on the other hand, takes direction into account. However, the magnitude of displacement (the distance from the starting point to the ending point) is represented using absolute value.
For example, if an object moves 5 meters to the right and then 3 meters to the left, the total distance traveled is |5| + |-3| = 8 meters. The displacement, however, is |5 - 3| = 2 meters to the right.
2. Computer Science and Programming: Error Handling and Data Validation
Absolute value is frequently used in computer programming for various purposes:
- Error Handling: In comparing floating-point numbers, a small difference within a certain tolerance is often considered negligible. Absolute value helps determine if the difference between two calculated values is within this acceptable margin of error.
- Data Validation: Absolute value can help enforce constraints on data input. For example, a program might require a value to be within a specific range. By comparing the absolute value of the input against the range limits, the program can identify invalid entries.
3. Statistics and Data Analysis: Measuring Deviation and Error
In statistics, absolute value is crucial for calculating various measures of deviation and error. For instance, the mean absolute deviation (MAD) and the mean absolute error (MAE) are common statistical metrics used to quantify the spread of data or the accuracy of predictions. These metrics rely heavily on the absolute value to ensure that positive and negative deviations are treated equally.
4. Finance and Economics: Measuring Risk and Volatility
Absolute value plays a role in financial modeling and analysis, especially when dealing with risk and volatility. For example, in portfolio management, the absolute deviations of returns from their expected values can be used to assess the risk associated with a particular investment strategy.
5. Geometry and Calculus: Distance Formula and Optimization Problems
The distance formula, a cornerstone of coordinate geometry, utilizes absolute value implicitly to calculate the distance between two points. This concept extends to more advanced calculus problems where optimization involves minimizing distances or absolute differences.
Addressing Common Misconceptions about Absolute Value
Several common misconceptions surround the absolute value function:
- Mistaking |x| for simply removing the negative sign: While this is true for negative numbers, it’s crucial to remember that |x| = x for non-negative x. It's not simply a matter of removing a minus sign.
- Incorrect application of distributive property: The absolute value does not distribute over addition or subtraction; that is, |x + y| ≠ |x| + |y| in general (though the triangle inequality provides an upper bound).
- Problems with solving absolute value equations and inequalities: Failing to consider both cases (positive and negative) when dealing with absolute value equations and inequalities leads to incomplete or incorrect solutions.
Expanding the Knowledge: Related Mathematical Concepts
Understanding absolute value provides a foundation for exploring more advanced mathematical concepts:
- Complex numbers: The absolute value extends to complex numbers, representing the distance of a complex number from the origin in the complex plane (also known as the modulus).
- Vector spaces: In linear algebra, the absolute value generalizes to the norm (or length) of a vector, a crucial concept in various applications.
- Metric spaces: The concept of distance, fundamental to absolute value, is formalized in metric spaces, which define a distance function satisfying certain properties.
Conclusion: The Significance of Absolute Value
While the absolute value of 16 might seem like a trivial calculation, the concept itself is anything but. Its simple definition belies a wealth of applications and deep connections to various areas of mathematics and beyond. From measuring distances in physics to handling errors in computer science, the absolute value function is a fundamental tool with far-reaching implications. By understanding its properties and applications, we gain a deeper appreciation for its significance in diverse fields and enhance our ability to solve complex mathematical problems. Therefore, the seemingly simple question "What is the absolute value of 16?" opens a gateway to a wider understanding of a fundamental concept in mathematics with pervasive real-world relevance.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Absolute Value Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.