What Is The Antiderivative Of 1 X 2
News Co
Apr 13, 2025 · 5 min read
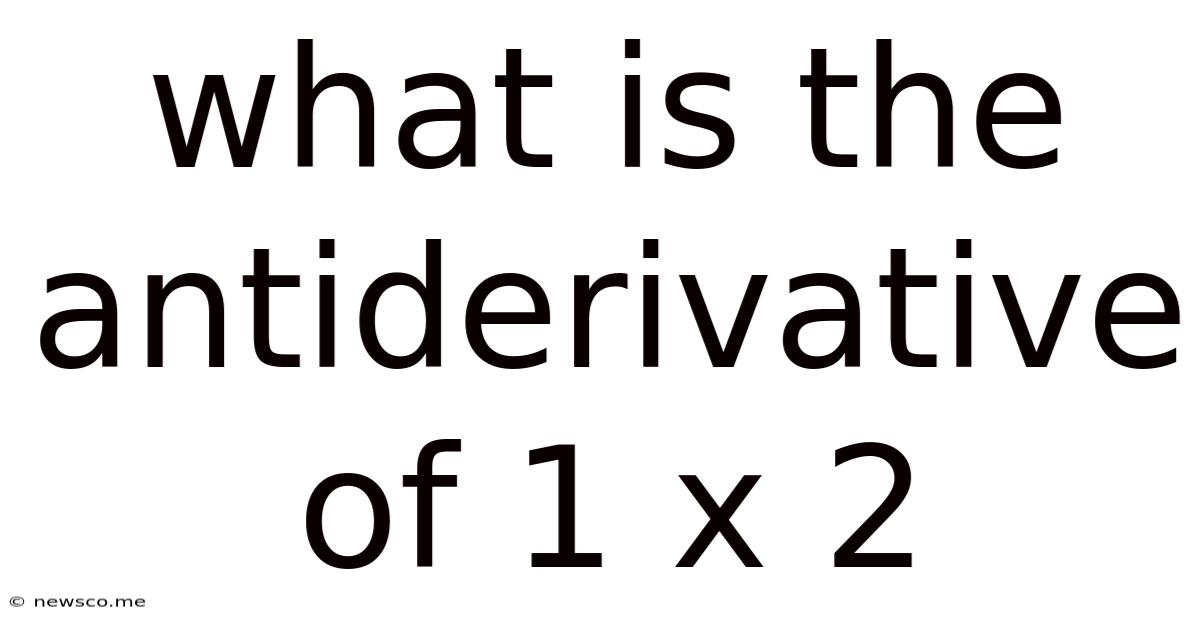
Table of Contents
What is the Antiderivative of 1/x²? A Comprehensive Guide
Finding the antiderivative of a function is a fundamental concept in calculus. It's the reverse process of differentiation, essentially asking, "What function, when differentiated, gives us this function?" This article delves into the intricacies of finding the antiderivative of 1/x², exploring various methods, clarifying common misconceptions, and providing a comprehensive understanding of this mathematical operation.
Understanding Antiderivatives
Before we tackle the specific problem of finding the antiderivative of 1/x², let's establish a solid foundation. The antiderivative, also known as the indefinite integral, represents a family of functions whose derivatives are the original function. We denote the antiderivative of a function f(x) as ∫f(x)dx. The 'dx' indicates that we're integrating with respect to the variable x. Importantly, the antiderivative is not a single function but a family of functions differing only by a constant. This constant, often represented as 'C', accounts for the fact that the derivative of a constant is always zero.
Key Concepts:
- Differentiation: The process of finding the derivative of a function, representing its instantaneous rate of change.
- Integration: The reverse process of differentiation, finding a function whose derivative is the given function.
- Indefinite Integral: The antiderivative, represented by ∫f(x)dx, representing a family of functions.
- Constant of Integration: The arbitrary constant 'C' added to the antiderivative, reflecting the fact that the derivative of a constant is zero.
Finding the Antiderivative of 1/x²
Now, let's address the core question: What is the antiderivative of 1/x²? We can rewrite 1/x² as x⁻². This form is more convenient for applying the power rule of integration.
The power rule of integration states: ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C, where n ≠ -1.
Applying this rule to our function x⁻²:
∫x⁻² dx = (x⁻²⁺¹)/(-2+1) + C = (x⁻¹)/(-1) + C = -x⁻¹ + C = -1/x + C
Therefore, the antiderivative of 1/x² is -1/x + C. The constant of integration, C, represents the family of functions that all have 1/x² as their derivative.
Graphical Representation and Verification
To visualize this, consider graphing several functions from the family -1/x + C, where C takes on different values. You'll notice that all these curves have the same slope at any given x-value, reflecting the fact that their derivatives are all the same (1/x²). The constant C simply shifts the entire curve vertically.
You can verify this result through differentiation. Take the derivative of -1/x + C:
d/dx (-1/x + C) = d/dx (-x⁻¹ + C) = x⁻² = 1/x²
This confirms that our antiderivative is correct.
Common Mistakes and Misconceptions
Several common errors can arise when finding the antiderivative of 1/x². Let's address some of them:
- Forgetting the Constant of Integration: This is perhaps the most frequent mistake. Remember that the antiderivative represents a family of functions, not a single function. Always include the constant of integration, 'C'.
- Incorrect Application of the Power Rule: The power rule does not apply when n = -1. The antiderivative of x⁻¹ (or 1/x) is ln|x| + C, not applying the standard power rule formula.
- Ignoring the Absolute Value in the Natural Logarithm: When integrating 1/x, the result is ln|x| + C. The absolute value is crucial because the natural logarithm is only defined for positive arguments. This is a significant point to remember and often overlooked.
Extending the Concept: Definite Integrals
While we've focused on indefinite integrals (antiderivatives), let's briefly touch on definite integrals. A definite integral calculates the area under a curve between two specified limits. It's denoted as ∫[a,b] f(x)dx, where 'a' and 'b' are the lower and upper limits of integration. The fundamental theorem of calculus connects definite and indefinite integrals:
∫[a,b] f(x)dx = F(b) - F(a), where F(x) is the antiderivative of f(x).
For our function, 1/x², finding the definite integral between limits a and b would involve:
∫[a,b] x⁻² dx = [-1/x]_[a,b] = (-1/b) - (-1/a) = 1/a - 1/b
Important Note: The definite integral of 1/x² will only be defined if neither 'a' nor 'b' is zero, as the function is undefined at x=0.
Practical Applications
Understanding antiderivatives, and specifically the antiderivative of 1/x², has numerous applications across various fields:
- Physics: Calculating work done by a variable force, analyzing motion under acceleration, and solving problems related to gravitational fields.
- Engineering: Determining the area under curves representing stress-strain relationships, calculating fluid flow, and solving differential equations in structural analysis.
- Economics: Modeling economic growth, determining marginal cost and revenue functions from cost and revenue functions, and analyzing consumer behavior.
- Probability and Statistics: Evaluating probability density functions and cumulative distribution functions.
Advanced Concepts and Related Topics
While this article primarily focuses on the basic integration of 1/x², several advanced concepts build upon this foundational understanding:
- Integration Techniques: More complex functions require advanced integration techniques such as integration by parts, substitution, and partial fraction decomposition.
- Improper Integrals: Integrals where one or both limits of integration are infinite.
- Multiple Integrals: Integrals involving more than one variable.
- Line Integrals and Surface Integrals: Integrals defined along curves or surfaces.
These advanced topics provide further avenues for understanding and applying integration techniques beyond the scope of this introductory guide.
Conclusion
Finding the antiderivative of 1/x² is a fundamental exercise in calculus. Understanding the process, applying the power rule correctly, and remembering the crucial constant of integration are essential for mastering this concept. The result, -1/x + C, forms the basis for numerous applications across diverse fields. By grasping this foundational concept, you pave the way for exploring more advanced aspects of calculus and its broad spectrum of applications in mathematics, science, and engineering. The ability to accurately find antiderivatives is a valuable skill for anyone studying or working in these fields. Remember to always check your work by differentiating your answer to verify that it returns the original function. Continuous practice and a solid understanding of the underlying principles are key to success in mastering this crucial calculus operation.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Antiderivative Of 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.