What Is The Common Multiple Of 12 And 16
News Co
Mar 29, 2025 · 5 min read
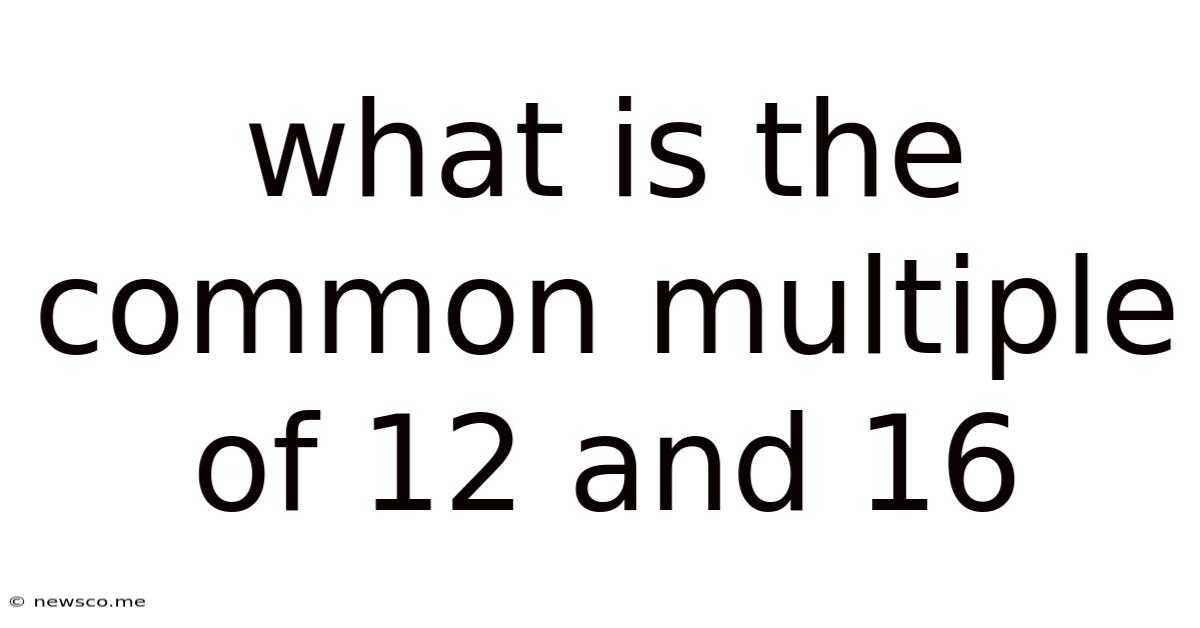
Table of Contents
What is the Least Common Multiple (LCM) of 12 and 16? A Deep Dive into Finding LCMs
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and algebra. It forms the bedrock for solving various problems, from simplifying fractions to scheduling events. This article will thoroughly explore how to find the LCM of 12 and 16, providing multiple methods and explaining the underlying principles. We'll also delve into the broader context of LCMs and their applications.
Understanding Least Common Multiples (LCMs)
Before we tackle the LCM of 12 and 16, let's solidify the definition. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. This means that if you divide the LCM by each of the original numbers, the result will always be a whole number (integer).
For example, let's consider the numbers 3 and 4. Multiples of 3 are 3, 6, 9, 12, 15, 18... Multiples of 4 are 4, 8, 12, 16, 20... The common multiples are the numbers that appear in both lists: 12, 24, 36, and so on. The least common multiple is the smallest of these common multiples, which is 12. Therefore, the LCM(3, 4) = 12.
Methods for Finding the LCM of 12 and 16
Several methods exist for determining the LCM of two numbers. Let's explore the most common ones, applying them to find the LCM(12, 16):
1. Listing Multiples Method
This is a straightforward approach, especially suitable for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 96, 108, 120...
- Multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128...
By comparing the lists, we see that the smallest number appearing in both is 48. Therefore, the LCM(12, 16) = 48. This method is simple but can become cumbersome for larger numbers.
2. Prime Factorization Method
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. This is a more efficient approach, especially for larger numbers.
- Prime factorization of 12: 2² × 3
- Prime factorization of 16: 2⁴
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2⁴ = 16
- The highest power of 3 is 3¹ = 3
Multiplying these highest powers together gives us the LCM: 16 × 3 = 48. Therefore, LCM(12, 16) = 48. This method is generally preferred for its efficiency and systematic approach.
3. Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) of two numbers are related through the following formula:
LCM(a, b) = (|a × b|) / GCD(a, b)
Where |a × b| represents the absolute value of the product of a and b. First, we need to find the GCD of 12 and 16. We can use the Euclidean algorithm for this:
- Divide 16 by 12: 16 = 12 × 1 + 4
- Divide 12 by the remainder 4: 12 = 4 × 3 + 0
The last non-zero remainder is the GCD, which is 4. Now, we can use the formula:
LCM(12, 16) = (12 × 16) / 4 = 192 / 4 = 48
Therefore, LCM(12, 16) = 48. This method is efficient and relies on a well-established algorithm for finding the GCD.
Applications of LCMs
The concept of LCMs has widespread applications across various fields:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires determining the LCM of the denominators.
-
Scheduling Problems: Imagine two buses departing from the same stop at different intervals. The LCM of their departure intervals determines when they will depart simultaneously again.
-
Cyclic Phenomena: LCMs are used to determine when periodic events, like planetary alignments or repeating patterns, will occur concurrently.
-
Modular Arithmetic: LCMs play a crucial role in solving problems in modular arithmetic, a branch of number theory.
-
Music Theory: LCMs are used in music theory to find the least common denominator of different rhythmic patterns and to harmonize musical intervals.
-
Computer Science: LCMs are used in various algorithms and data structures, especially in problems related to scheduling and resource allocation.
Beyond the Basics: LCMs of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you simply consider the highest power of each prime factor present in all the factorizations. For the GCD method, you can extend the Euclidean algorithm to handle multiple numbers. However, listing multiples becomes increasingly impractical with more numbers.
Conclusion: Mastering the LCM of 12 and 16 and Beyond
Finding the LCM of 12 and 16, as we've demonstrated, is achievable through several methods. The prime factorization method is generally the most efficient and systematic approach, particularly when dealing with larger numbers. Understanding the concept of LCM and its various applications is crucial for anyone pursuing mathematics or related fields. This comprehensive exploration provides a solid foundation for tackling more complex LCM problems and understanding their significance in various mathematical and real-world contexts. Remember to practice these methods to solidify your understanding and build your problem-solving skills. The ability to efficiently calculate LCMs is a valuable tool in your mathematical arsenal.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Common Multiple Of 12 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.