What Is The Cube Root Of 2
News Co
Apr 04, 2025 · 5 min read
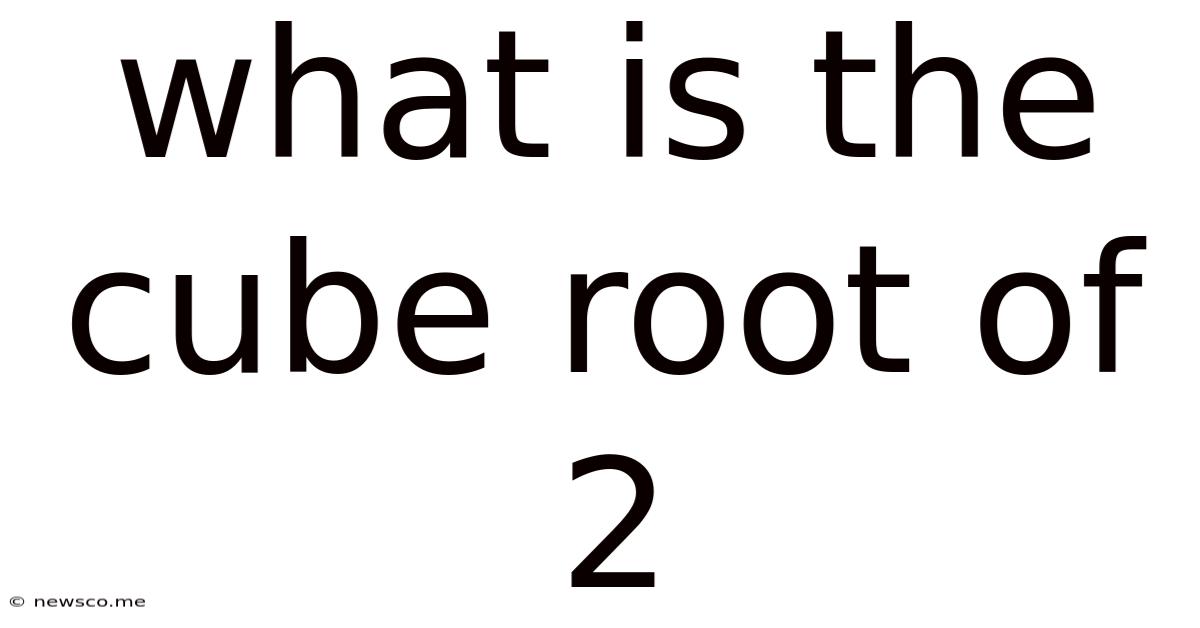
Table of Contents
What is the Cube Root of 2? Exploring a Fundamental Mathematical Concept
The cube root of 2, denoted as <sup>3</sup>√2 or 2<sup>⅓</sup>, is a fundamental concept in mathematics with far-reaching implications across various fields. Understanding its nature, calculation, and applications is crucial for anyone pursuing a deeper understanding of numerical analysis, algebra, and even advanced physics. This comprehensive article will delve into the intricacies of the cube root of 2, exploring its definition, methods of approximation, its significance in different mathematical contexts, and its practical applications.
Defining the Cube Root of 2
The cube root of 2 is the number which, when multiplied by itself three times (cubed), equals 2. In simpler terms, it's the solution to the equation x³ = 2. Unlike the cube root of perfect cubes like 8 (which is 2 because 2 x 2 x 2 = 8), the cube root of 2 is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers) and its decimal representation continues infinitely without repeating.
This seemingly simple number holds a significant position in mathematics, acting as a cornerstone for various concepts and calculations. Its irrational nature necessitates the use of approximation methods to obtain its value to a desired level of accuracy.
Approximating the Cube Root of 2: Various Methods
Several methods exist for approximating the cube root of 2, each varying in complexity and accuracy. Here, we will examine some of the most common approaches:
1. Using a Calculator or Computer Software
The simplest method involves using a calculator or a computer software program with a built-in cube root function. These tools provide a highly accurate approximation, typically up to several decimal places. For instance, a calculator will give you an approximation like 1.259921...
While convenient, this method lacks the understanding of the underlying mathematical principles. It's crucial to understand how such approximations are derived.
2. The Babylonian Method (Newton-Raphson Method)
This iterative method is a powerful technique for finding the roots of equations, including cube roots. It refines an initial guess through successive approximations, converging towards the true value. The formula for the Babylonian method applied to finding the cube root of a number 'a' is:
x<sub>n+1</sub> = (1/3) * (2x<sub>n</sub> + a/x<sub>n</sub>²)
where x<sub>n</sub> is the nth approximation and x<sub>n+1</sub> is the next approximation.
Let's apply this to find the cube root of 2. We can start with an initial guess of x<sub>0</sub> = 1.
- Iteration 1: x<sub>1</sub> = (1/3) * (2(1) + 2/1²) = 4/3 ≈ 1.3333
- Iteration 2: x<sub>2</sub> = (1/3) * (2(4/3) + 2/(4/3)²) ≈ 1.2639
- Iteration 3: x<sub>3</sub> = (1/3) * (2(1.2639) + 2/(1.2639)²) ≈ 1.2599
As you can see, the approximation rapidly converges towards the true value of the cube root of 2 with each iteration. The more iterations you perform, the greater the accuracy.
3. Binomial Theorem Approximation
The binomial theorem can be used to approximate the cube root of 2. This method involves expressing 2 as (1 + 1) and using the binomial series expansion for (1+x)<sup>⅓</sup>. While mathematically elegant, this method is more complex than the Babylonian method and requires a good understanding of binomial series expansions.
4. Numerical Methods (e.g., Bisection Method, Secant Method)
More advanced numerical methods, such as the bisection method and the secant method, provide systematic approaches to finding the roots of equations. These methods are often employed in computer algorithms to calculate highly accurate approximations.
The Significance of the Cube Root of 2 in Mathematics
The cube root of 2 plays a significant role in various mathematical contexts:
-
Geometry: It appears in geometrical problems involving cubes, volumes, and three-dimensional spaces. For instance, it's related to the side length of a cube with a volume of 2 cubic units.
-
Algebra: It is a fundamental example of an irrational number, illustrating the concept of numbers that cannot be expressed as a ratio of two integers. Its properties are studied within the framework of field extensions and algebraic number theory.
-
Calculus: The cube root function (f(x) = x<sup>⅓</sup>) is a common example used to illustrate concepts such as derivatives and integrals. Its derivative and integral are straightforward to calculate, providing good examples for students learning calculus.
-
Number Theory: The cube root of 2 is an algebraic number, which means it's a root of a polynomial equation with integer coefficients. Its properties within the field of algebraic numbers are a topic of significant interest in number theory.
-
Abstract Algebra: The cube root of 2 is crucial in studying field extensions. It helps illustrate the concepts of minimal polynomials and algebraic degrees within abstract algebra.
Applications of the Cube Root of 2 in Real-World Scenarios
While not as prominent as other mathematical constants like π or e, the cube root of 2 finds applications in several real-world situations:
-
Engineering and Physics: In engineering and physics problems involving volume calculations, the cube root of 2 can appear in determining dimensions. For example, calculating the side length of a cube with a specific volume.
-
Computer Graphics and Simulations: The cube root of 2 might be used in various 3D modeling and simulation applications requiring precise volume calculations or spatial relationships.
-
Financial Modeling: In certain financial models involving compound interest or growth rates, the cube root function can be employed to calculate growth factors or investment timelines.
Conclusion: Understanding the Depth of a Simple Number
The cube root of 2, while appearing as a simple mathematical expression, encapsulates profound mathematical concepts and possesses surprising applications across various fields. Understanding its irrational nature, different approximation methods, and its role in various mathematical branches provides a deeper appreciation for the complexity and elegance of mathematical structures. From its geometric interpretations to its applications in numerical analysis and beyond, the cube root of 2 serves as a testament to the interconnectedness of mathematical ideas and their relevance to the real world. By grasping the essence of this seemingly simple number, we gain a more substantial foundation for tackling more complex mathematical challenges and appreciating the richness of the mathematical landscape.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Cube Root Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.