What Is The Derivative Of Ln2x
News Co
Apr 01, 2025 · 5 min read
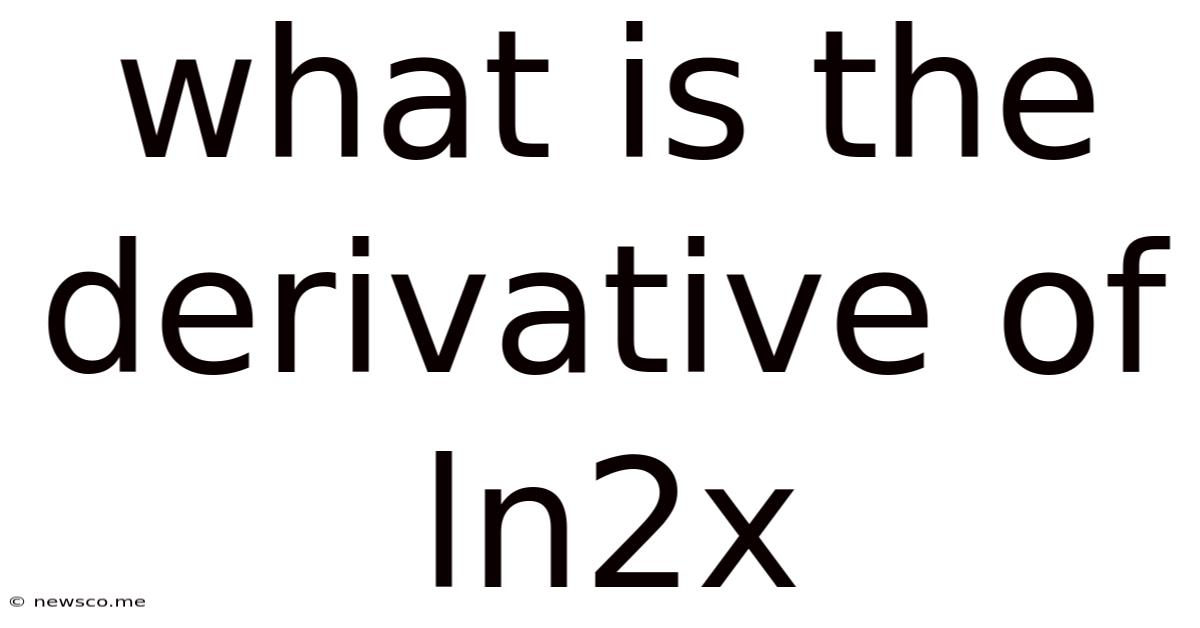
Table of Contents
What is the Derivative of ln(2x)? A Comprehensive Guide
The derivative of ln(2x) is a fundamental concept in calculus, frequently encountered in various applications. Understanding how to derive this, and more importantly, why the process works, is crucial for mastering more advanced calculus concepts. This comprehensive guide will delve into the derivation, explore its applications, and provide you with a solid understanding of this essential mathematical operation.
Understanding the Fundamentals: Logarithms and Derivatives
Before we jump into the derivative of ln(2x), let's refresh our understanding of the key concepts involved:
What is a Logarithm?
A logarithm is the inverse function of exponentiation. In simpler terms, if b<sup>x</sup> = y, then log<sub>b</sub>(y) = x. Here, 'b' is the base of the logarithm. The natural logarithm (ln) uses the mathematical constant e (approximately 2.71828) as its base. Therefore, ln(x) is equivalent to log<sub>e</sub>(x).
What is a Derivative?
In calculus, the derivative of a function represents its instantaneous rate of change at any given point. Geometrically, it represents the slope of the tangent line to the function's graph at that point. The process of finding the derivative is called differentiation.
Deriving the Derivative of ln(2x) using the Chain Rule
The derivative of ln(2x) requires the application of the chain rule, a crucial rule in differentiation. The chain rule states that the derivative of a composite function is the derivative of the outer function (with the inside function left alone) times the derivative of the inner function.
Let's break down the derivation step-by-step:
-
Identify the composite function: ln(2x) is a composite function. The outer function is ln(u) and the inner function is u = 2x.
-
Apply the chain rule: The chain rule formula is: d/dx [f(g(x))] = f'(g(x)) * g'(x)
-
Differentiate the outer function: The derivative of ln(u) with respect to u is 1/u.
-
Differentiate the inner function: The derivative of 2x with respect to x is 2.
-
Combine the results: Applying the chain rule, we get:
d/dx [ln(2x)] = (1/(2x)) * 2 = 1/x
Therefore, the derivative of ln(2x) is 1/x.
Alternative Derivation using Logarithmic Properties
We can also derive the derivative using logarithmic properties. Recall that ln(ab) = ln(a) + ln(b). Using this property, we can rewrite ln(2x) as:
ln(2x) = ln(2) + ln(x)
Now, differentiate term by term:
d/dx [ln(2x)] = d/dx [ln(2)] + d/dx [ln(x)]
Since ln(2) is a constant, its derivative is 0. The derivative of ln(x) is 1/x. Therefore:
d/dx [ln(2x)] = 0 + 1/x = 1/x
This method confirms our previous result.
Applications of the Derivative of ln(2x)
The derivative of ln(2x), 1/x, has widespread applications across various fields, including:
-
Optimization Problems: In optimization problems, finding the maximum or minimum of a function often involves setting its derivative equal to zero. If ln(2x) is part of the function, its derivative plays a crucial role in this process.
-
Related Rates Problems: These problems involve finding the rate of change of one quantity with respect to another. The derivative of ln(2x) may be needed when dealing with functions involving logarithmic growth or decay.
-
Economics and Finance: Logarithmic functions are frequently used in modeling economic growth, compound interest, and other financial phenomena. The derivative provides insights into the rate of growth or decay of these quantities.
-
Physics and Engineering: Logarithmic functions appear in various physics and engineering contexts, such as in the study of radioactive decay, signal processing, and thermodynamics. Their derivatives are essential for understanding rates of change in these systems.
-
Probability and Statistics: Logarithms are used in probability and statistics to simplify calculations involving probabilities and likelihoods. Their derivatives are vital in analyzing these statistical models and making inferences.
Understanding the Significance of the Result: 1/x
The result, 1/x, is significant because it demonstrates a fundamental property of logarithmic functions. The derivative of the natural logarithm of a function is the reciprocal of that function, multiplied by its derivative (in the case of a composite function, as seen in our example). This property is incredibly useful in solving various problems. It highlights the inverse relationship between exponential and logarithmic functions.
Common Mistakes to Avoid
When calculating derivatives, especially those involving composite functions, several common mistakes can occur:
-
Forgetting the chain rule: This is the most frequent error. Always remember to multiply by the derivative of the inner function when dealing with composite functions.
-
Incorrect application of logarithmic properties: Make sure to correctly apply logarithmic properties such as ln(ab) = ln(a) + ln(b) and ln(a/b) = ln(a) - ln(b).
-
Errors in simplification: After applying the chain rule and logarithmic properties, carefully simplify the expression to obtain the final derivative.
-
Confusing the derivative of ln(x) with the derivative of e<sup>x</sup>: These are inverse functions, and their derivatives are different. Remember that d/dx[ln(x)] = 1/x and d/dx[e<sup>x</sup>] = e<sup>x</sup>.
Further Exploration: Derivatives of More Complex Logarithmic Functions
The principles discussed above can be extended to more complex logarithmic functions. For instance:
-
ln(ax + b): Using the chain rule, the derivative is a/(ax + b).
-
ln(f(x)): The derivative is f'(x)/f(x).
-
ln(√x): Rewriting as ln(x<sup>1/2</sup>) = (1/2)ln(x), the derivative is 1/(2x).
By understanding the fundamental concepts and applying the chain rule correctly, you can confidently tackle the derivatives of a wide range of logarithmic functions. Mastering these skills is essential for success in calculus and its applications across various fields.
Conclusion
The derivative of ln(2x) is 1/x. This seemingly simple result arises from a combination of fundamental calculus concepts and the powerful chain rule. Understanding its derivation and applications provides a solid foundation for tackling more complex problems in calculus and related fields. Remember to practice regularly and pay close attention to detail to avoid common mistakes. With consistent effort, you will master the derivative of ln(2x) and its applications. This understanding will serve as a stepping stone to further explorations in the fascinating world of calculus.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Derivative Of Ln2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.